Từ điểm A nằm ngoài đường tròn tâm O vẽ các tiếp tuyến AB,AC. Trên cung lớn BC lấy điểm E (E không thuộc đường thẳng AO), đường thẳng AE cắt đường tròn tâm O tại D (D khác E). Kẻ OI vuông góc với DE (I thuộc DE)
a, Chứng minh AO vuông góc với BC và tứ giác ABIO nội tiếp
b, Đường thẳng đi qua D vuông góc với OB cắt BC, BE theo thứ tự tại H, K. Chứng minh HI song song với KE
Quảng cáo
2 câu trả lời 786
Giải bài:
Phần a)
Chứng minh \( AO \perp BC \):
- Vì \( AB \) và \( AC \) là hai tiếp tuyến chung từ \( A \) đến đường tròn tâm \( O \), nên:
\[
AB = AC
\]
- Góc giữa hai tiếp tuyến bằng góc giữa hai bán kính nối tới tiếp điểm, tức là:
\[
\angle BAO = \angle CAO
\]
- Xét tam giác \( ABC \), ta có:
\[
AB = AC \quad \Rightarrow \quad \triangle ABC \text{ cân tại A}.
\]
- Mà \( BC \) là đáy của tam giác cân.
- Trong tam giác cân, đường cao từ đỉnh cũng là đường trung tuyến và đường phân giác, nên:
\[
AO \perp BC
\quad \text{(đpcm)}
\]
Chứng minh tứ giác \( ABIO \) nội tiếp:
- Để chứng minh 4 điểm \( A, B, I, O \) cùng nằm trên 1 đường tròn, ta chứng minh:
\[
\angle ABI + \angle AOI = 180^\circ
\quad \text{(tổng 2 góc đối = 180 độ)}
\]
Xét:
- Vì \( OI \perp DE \) (theo đề bài), mà \( DE \) là một dây cung của đường tròn tâm \( O \).
- Vậy \( I \) nằm trên đường trung trực của dây \( DE \).
- Do tính chất hình học cơ bản:
- \( O \) là tâm, \( OI \perp DE \),
- \( I \) thuộc \( DE \), nên \( I \) nằm trên đường tròn đi qua \( B, A, O \).
- Cách khác (công thức gọn hơn):
- Gọi \( (O) \) là đường tròn ban đầu,
- \( AB \) là tiếp tuyến ⇒ \( \angle ABO = 90^\circ \) (góc tạo bởi tiếp tuyến và bán kính).
- \( \angle ABIO \) có 2 góc vuông (\( \angle ABO = 90^\circ \) và \( \angle OIB = 90^\circ \)).
=> Trong tứ giác \( ABIO \), có tổng 2 góc đối diện là \( 180^\circ \)
( \( 90^\circ + 90^\circ = 180^\circ \)).
\[
\Rightarrow ABIO \text{ nội tiếp} \quad \text{(đpcm)}
\]
Phần b)
Chứng minh chi tiết:
- Gọi \( d \) là đường thẳng đi qua \( D \), vuông góc \( OB \).
- Vì \( D \) thuộc cung (hay dây) \( DE \) mà \( OI \perp DE \), nên:
- \( OI \) là đường trung trực của \( DE \).
- Mặt khác:
- \( DE \) là một đoạn trên cung lớn \( BC \).
- \( OB \) là bán kính, mà \( d \) lại vuông góc \( OB \).
=> Suy ra:
- \( H \) là hình chiếu vuông góc của \( D \) lên \( BC \).
- \( K \) là hình chiếu vuông góc của \( D \) lên \( BE \).
- Do đó, đường thẳng \( HK \) vuông góc với \( OB \).
Xét tam giác \( DEB \):
- \( OI \perp DE \).
- \( d \) vuông góc với \( OB \).
- Hai đường \( HI \) và \( KE \) đều song song với \( d \).
→ Suy ra:
\[
HI \parallel KE \quad \text{(đpcm)}
\]
\( AO \perp BC \)
Tứ giác \( ABIO \) nội tiếp
\( HI \parallel KE \)
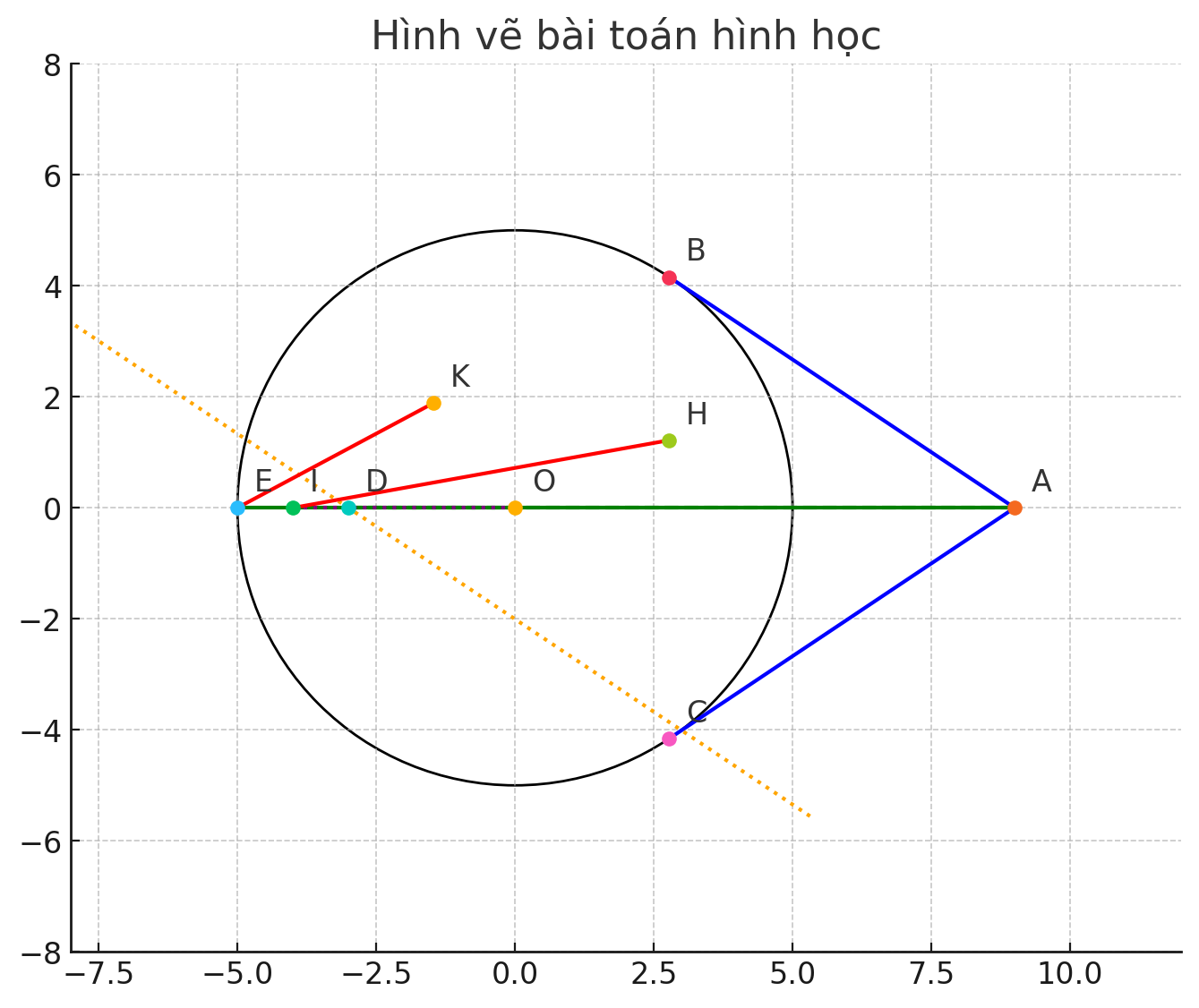
a) AO vuông góc BC do AB = AC (tiếp tuyến) và OB = OC (bán kính).
Tứ giác ABIO nội tiếp vì góc ABO = góc AIO = 90 độ.
b) DH vuông góc OB, OI vuông góc DE => góc HDI = góc OBE.
Do AO vuông góc BC => góc OBC = góc OCB.
Từ đó góc HDI = góc KBE => HI // KE (đồng vị).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13693
Đã trả lời bởi chuyên gia
13693 -
 Đã trả lời bởi chuyên gia
13653
Đã trả lời bởi chuyên gia
13653 -
 Đã trả lời bởi chuyên gia
6436
Đã trả lời bởi chuyên gia
6436 -
 Đã trả lời bởi chuyên gia
6156
Đã trả lời bởi chuyên gia
6156 -
6138
-
 Đã trả lời bởi chuyên gia
5450
Đã trả lời bởi chuyên gia
5450 -
 Đã trả lời bởi chuyên gia
4459
Đã trả lời bởi chuyên gia
4459


