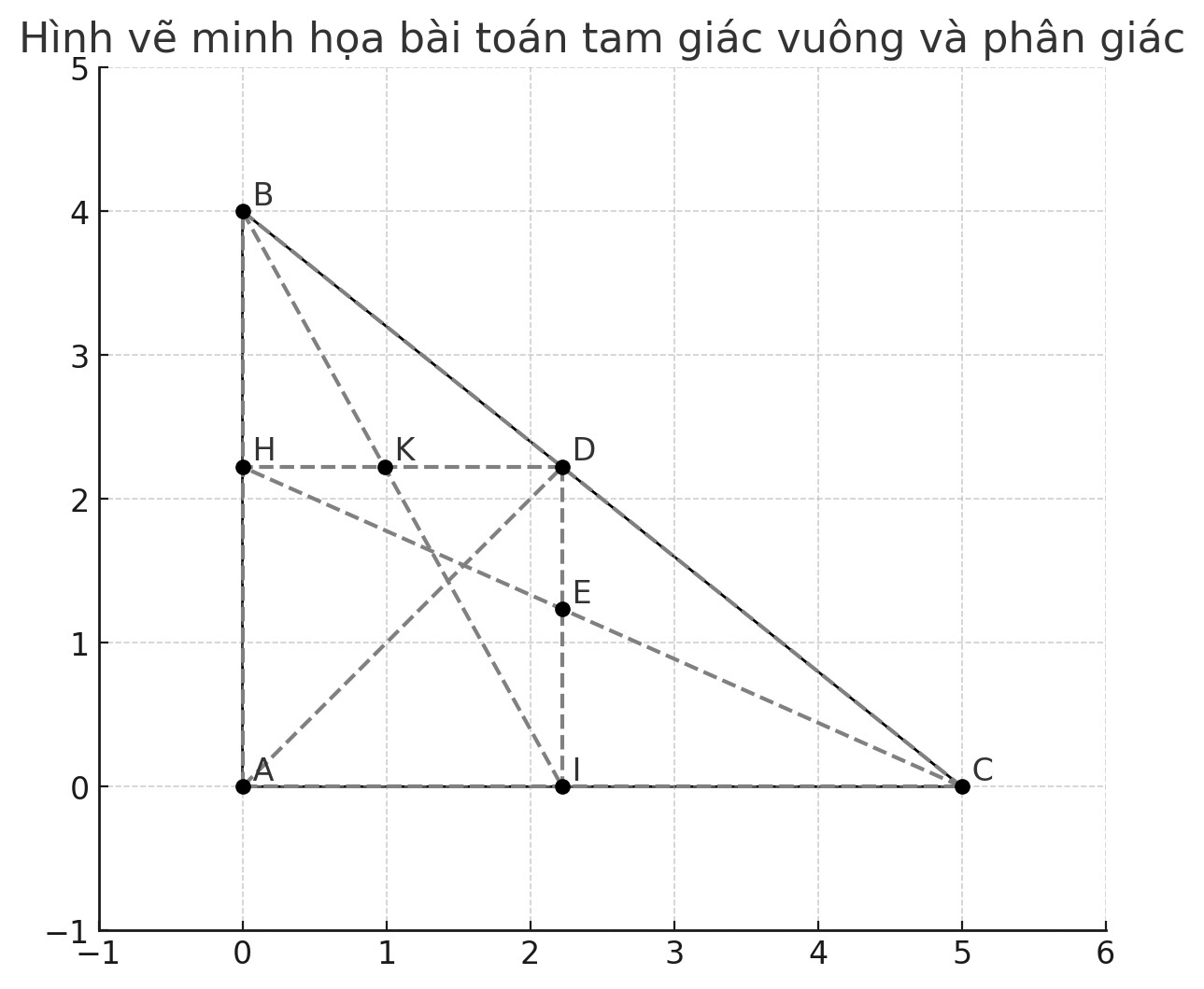
1. Chứng minh tứ giác \(AHDI\) là hình vuông

- Ta có:
- \(DH \perp AB\), suy ra góc \(AHD = 90^\circ\).
- \(DI \perp AC\), suy ra góc \(AID = 90^\circ\).
- Tam giác \(ABC\) vuông tại \(A\), suy ra góc \(H A I = 90^\circ\).

⇒ Tứ giác \(AHDI\) có ba góc vuông tại \(H, I, A\), do đó góc còn lại tại \(D\) cũng là góc vuông (360° - 270° = 90°).

⇒ \(AHDI\) là hình chữ nhật.

- Xét hai tam giác vuông \(AHD\) và \(AID\):

+ Có chung cạnh huyền \(AD\).
+ Chung góc \(\angle HAD = \angle IAD\) (vì \(AD\) là tia phân giác góc \(BAC\)).

⇒ Hai tam giác vuông này bằng nhau (cạnh huyền - góc nhọn).

Suy ra:
\[
AH = AI
\]

- Tứ giác \(AHDI\) là hình chữ nhật có hai cạnh kề \(AH = AI\), nên đây là hình vuông.

2. Chứng minh tam giác \(AHC\) đồng dạng với tam giác \(HKA\)

- Xét hai tam giác: \(AHC\) và \(HKA\).

- Góc chung:
- Hai tam giác \(AHC\) và \(HKA\) cùng có góc tại đỉnh \(A\), cụ thể:
\[
\angle HAC \quad(\text{của tam giác }AHC) = \angle KAH \quad(\text{của tam giác }HKA)
\]
vì thực chất đây là cùng một góc \(HA\) chung giữa hai tam giác.

- Xét góc vuông:
- Ta đã có \(AH \perp DH\), nên góc \(\angle AHD = 90^\circ\). Tứ giác \(AHDI\) là hình vuông nên góc tại \(H\) của tam giác \(HKA\) (góc \(AHK\)) là 90°.
- Góc tại \(H\) của tam giác \(AHC\) là góc \(AHC\), cần xét xem góc này có bằng góc nào tương ứng trong tam giác \(HKA\) hay không:

Thực tế, ta nhận thấy rằng:
- Tứ giác \(AHDI\) là hình vuông, suy ra cạnh \(AH\parallel DI\), do đó \(CH\) và \(DI\) cắt nhau tại \(E\), dẫn đến góc \(AHC\) chính bằng góc \(KHA\) (hai góc đối đỉnh tại \(H\) vì hai cặp đường thẳng \(AH\), \(DI\) song song và \(CH\), \(DH\) cắt nhau).

- Như vậy, ta có:
\[
\angle HAC = \angle KAH,\quad \angle AHC = \angle KHA
\]

- Từ đó, hai tam giác \(AHC\) và \(HKA\) đồng dạng theo tiêu chí góc - góc (g.g).

Ta có tam giác ABC vuông tại A nên AD là đường cao của tam giác ABC.
Do đó, ta có:
$\angle AHD = 90^{\circ}$ và $\angle ADH = 90^{\circ}$.
Vậy tứ giác AHDI là hình vuông.

Gọi E là giao điểm của AI và BC.
Ta có $\angle BAI = \angle CAE$ (cùng là góc ngoại tiếp trên cùng cạnh AC).
Vậy tứ giác AECB là tứ giác nội tiếp.
Do đó, ta có $\angle AEC = \angle ABC$ và $\angle ACE = \angle ACB$.

Xét tam giác AHD vuông tại H, ta có:
$\frac{HD}{HA} = \cos \angle AHD = \cos \angle ABC$ (1).

Xét tam giác AEC, ta có:
$\frac{EC}{EA} = \cos \angle ACE = \cos \angle ACB$ (2).

Từ (1) và (2), ta có:
$\frac{HD}{HA} = \frac{EC}{EA}$.
Vậy ta có $\frac{HD}{HA} = \frac{EC}{EA}$ hay $\frac{HD}{EC} = \frac{HA}{EA}$.

Xét tam giác AIB, ta có:
$\frac{HB}{HA} = \frac{\sin \angle HAI}{\sin \angle HIA}$.

Xét tam giác AIC, ta có:
$\frac{EC}{EA} = \frac{\sin \angle EAI}{\sin \angle AIE}$.

Vậy ta có:
$\frac{HB}{HA} = \frac{\sin \angle HAI}{\sin \angle HIA} = \frac{\sin \angle EAI}{\sin \angle AIE} = \frac{HD}{EC}$.

Vậy ta có $\frac{HB}{HA} = \frac{HD}{EC}$ hay $\frac{HB}{HA} = \frac{HD}{EC} = \frac{HA}{EA}$.

Vậy ta có $\frac{HB}{HA} = \frac{HD}{EC} = \frac{HA}{EA}$ hay $\frac{HB}{HA} = \frac{HD}{EC} = \frac{HA}{EA} = \frac{KD}{KC}$. Điều phải chứng minh.
Thu gọn (-)

Ta có tam giác ABC vuông tại A nên AD là đường cao của tam giác ABC.
Do đó, ta có:
$\angle AHD = 90^{\circ}$ và $\angle ADH = 90^{\circ}$.
Vậy tứ giác AHDI là hình vuông.

Gọi E là giao điểm của AI và BC.
Ta có $\angle BAI = \angle CAE$ (cùng là góc ngoại tiếp trên cùng cạnh AC).
Vậy tứ giác AECB là tứ giác nội tiếp.
Do đó, ta có $\angle AEC = \angle ABC$ và $\angle ACE = \angle ACB$.

Xét tam giác AHD vuông tại H, ta có:
$\frac{HD}{HA} = \cos \angle AHD = \cos \angle ABC$ (1).

Xét tam giác AEC, ta có:
$\frac{EC}{EA} = \cos \angle ACE = \cos \angle ACB$ (2).

Từ (1) và (2), ta có:
$\frac{HD}{HA} = \frac{EC}{EA}$.
Vậy ta có $\frac{HD}{HA} = \frac{EC}{EA}$ hay $\frac{HD}{EC} = \frac{HA}{EA}$.

Xét tam giác AIB, ta có:
$\frac{HB}{HA} = \frac{\sin \angle HAI}{\sin \angle HIA}$.

Xét tam giác AIC, ta có:
$\frac{EC}{EA} = \frac{\sin \angle EAI}{\sin \angle AIE}$.

Vậy ta có:
$\frac{HB}{HA} = \frac{\sin \angle HAI}{\sin \angle HIA} = \frac{\sin \angle EAI}{\sin \angle AIE} = \frac{HD}{EC}$.

Vậy ta có $\frac{HB}{HA} = \frac{HD}{EC}$ hay $\frac{HB}{HA} = \frac{HD}{EC} = \frac{HA}{EA}$.

Vậy ta có $\frac{HB}{HA} = \frac{HD}{EC} = \frac{HA}{EA}$ hay $\frac{HB}{HA} = \frac{HD}{EC} = \frac{HA}{EA} = \frac{KD}{KC}$. Điều phải chứng minh.