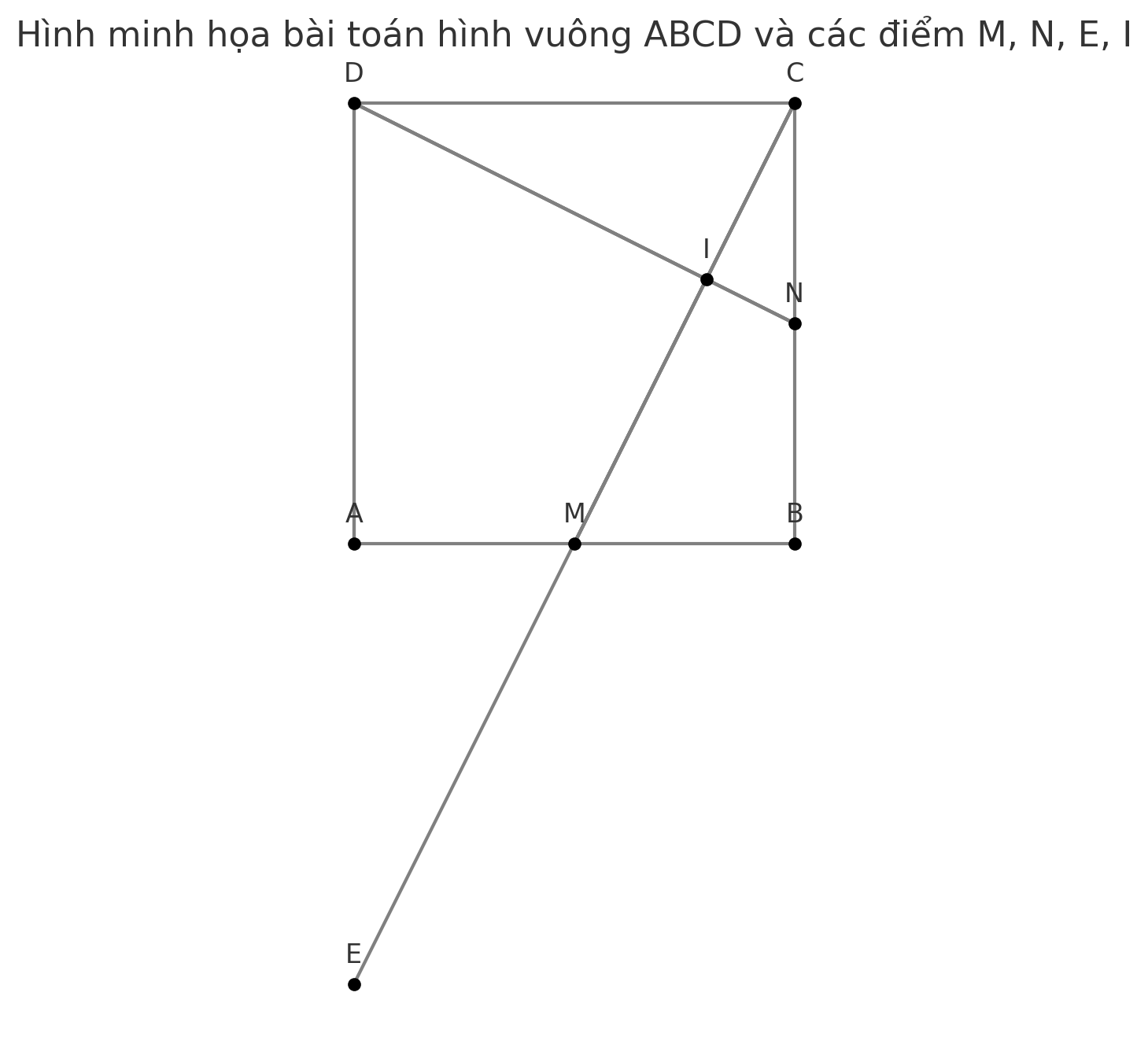
a) Tính độ dài đoạn DN

Gán tọa độ:
- \( A(0, 0) \), \( B(4, 0) \), \( C(4, 4) \), \( D(0, 4) \)

Tọa độ điểm:
- \( M \): trung điểm \( AB \) → \( M = \left( \frac{0 + 4}{2}, 0 \right) = (2, 0) \)
- \( N \): trung điểm \( BC \) → \( N = \left( \frac{4 + 4}{2}, \frac{0 + 4}{2} \right) = (4, 2) \)
- \( D = (0, 4) \)

Độ dài đoạn \( DN \):

\[
DN = \sqrt{(4 - 0)^2 + (2 - 4)^2} = \sqrt{16 + 4} = \sqrt{20} = 2\sqrt{5} \, \text{cm}
\]

Vậy: \( DN = 2\sqrt{5} \, \text{cm} \)

b) Chứng minh \( DN \perp CE \)

Ta chứng minh 2 vector \( \vec{DN} \) và \( \vec{CE} \) vuông góc ⇔ tích vô hướng = 0

Tọa độ điểm \( E \):

- \( MC \): đi qua \( M(2, 0) \) và \( C(4, 4) \)
- \( AD \): đi qua \( A(0, 0) \) và \( D(0, 4) \)

→ \( AD \) là đường thẳng dọc: \( x = 0 \)
→ Tìm giao điểm \( E \) của đường MC với \( x = 0 \)

Phương trình MC: qua \( (2, 0) \), \( (4, 4) \)
→ Hệ số góc \( m = \frac{4 - 0}{4 - 2} = 2 \)
→ Phương trình: \( y = 2(x - 2) = 2x - 4 \)

Thay \( x = 0 \):
→ \( y = -4 \) ⇒ \( E(0, -4) \)

- \( \vec{DN} = (4 - 0, 2 - 4) = (4, -2) \)
- \( \vec{CE} = (0 - 4, -4 - 4) = (-4, -8) \)

Tích vô hướng:

\[
\vec{DN} \cdot \vec{CE} = 4 \cdot (-4) + (-2) \cdot (-8) = -16 + 16 = 0
\]

Vậy \( DN \perp CE \)