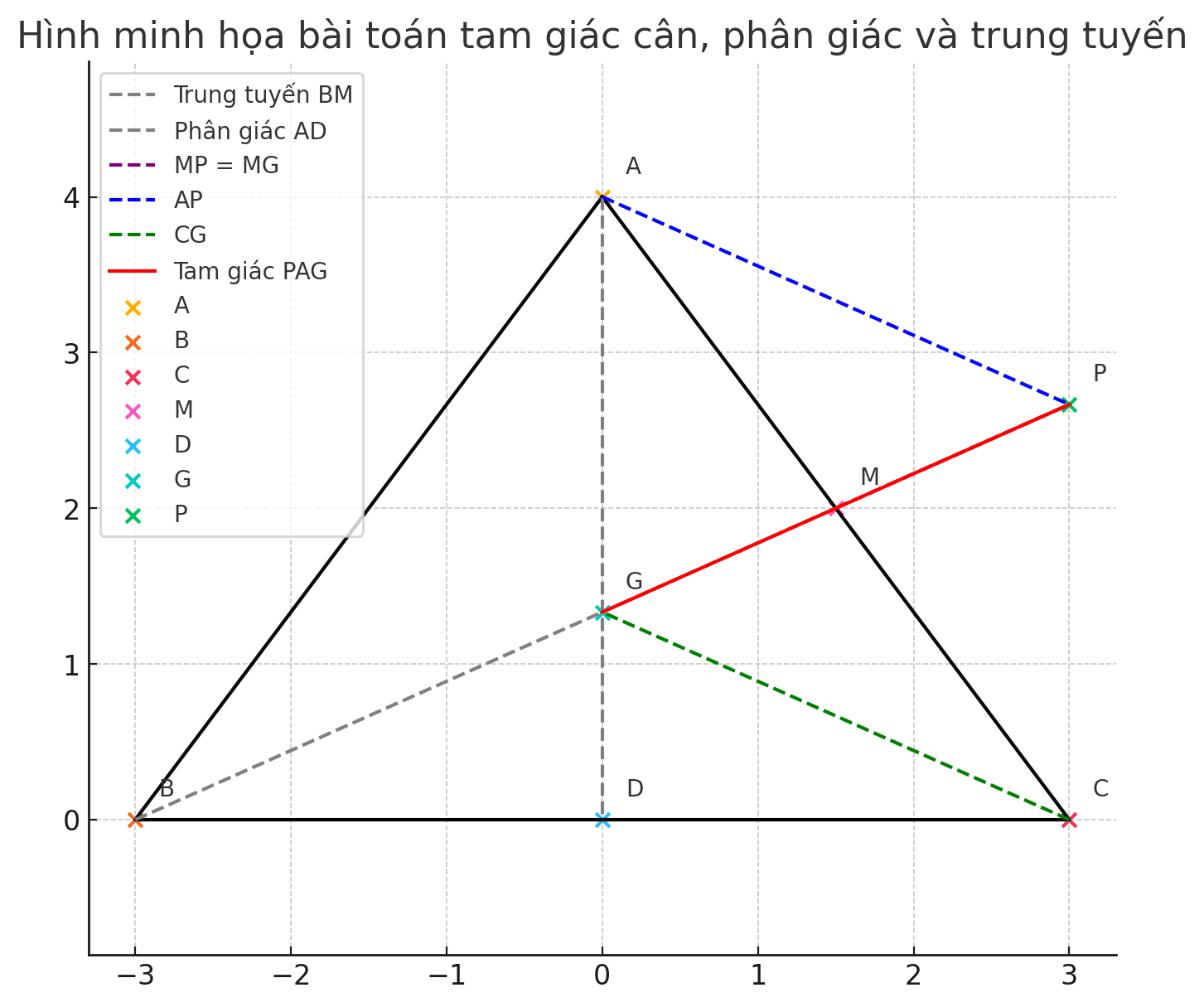
Câu 15. (2,5 điểm) Cho tam giác ABC cân tại A , tia phân giác (AD ) và đường trung tuyến (BM ) cắt nhau tạiG .
a) Chứng minh .ABD=ACD
b) Trên tia đối của tiaMB lấy điểmP sao cho MP=MG. Chứng minh .AP=CG
c) Chứng minh PAG cân.
Quảng cáo
1 câu trả lời 881
a) Chứng minh ∠ABD = ∠ACD
Vì AD là phân giác của góc BAC ⇒
⇒ Góc ∠BAD = ∠CAD (1)
Tam giác ABC cân tại A ⇒ AB = AC (2)
Trong hai tam giác ABD và ACD:
- AB = AC (tam giác cân)
- ∠BAD = ∠CAD (từ (1))
- AD chung
⇒ Tam giác ABD = tam giác ACD (c.g.c)
⇒ Suy ra: ∠ABD = ∠ACD (hai góc tương ứng)
∠ABD = ∠ACD
b) Trên tia đối của tia MB lấy điểm P sao cho MP = MG. Chứng minh AP = CG
Giả sử MP = MG, mà P nằm trên tia đối của MB, nên điểm P và điểm G nằm đối xứng nhau qua điểm M.
⇒ M là trung điểm của PG ⇒ PG đối xứng nhau qua M
Từ đó, ta có các cặp đoạn đối xứng:
- MP = MG (giả thiết)
- M là trung điểm của AC (do BM là trung tuyến)
⇒ Ta có:
- A, P đối xứng với C, G qua M
⇒ AP = CG
AP = CG
c) Chứng minh tam giác PAG cân
Từ trên đã có:
- AP = CG
- M là trung điểm của cả AC và PG
⇒ A và G đối xứng nhau qua M
⇒ Tam giác PAG có AP = AG (do đối xứng)
⇒ Tam giác PAG cân tại P
Tam giác PAG cân tại P
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12381
-
 Đã trả lời bởi chuyên gia
5734
Đã trả lời bởi chuyên gia
5734 -
4829


