cho nữa đường tròn (O;R) , đường kính AB. Gọi Ax , By là các tiếp tuyến của nữa...

Question

cho nữa đường tròn (O;R) , đường kính AB. Gọi Ax , By là các tiếp tuyến của nữa đường tròn (Ax, By và nũa đường tròn thuộc cùng nữa mặt phẳng có bờ là đường thẳng chứa AB). Từ điểm M trên nữa đường tròn (M khác A , B)vẽ tiếp tuyến với nữa đường tròn, tiếp tuyến này cắt Ax và By lần lượt là C và D
a) cm tứ giác ACMO nội tiếp
b) chứng minh OC .MB = OD . MA
c) gọi H là hình chiếu của M trên AB . Chứng minh AD cắt MH tại I là trung điểm MH

VietJack · Accepted Answer

Xem đáp án từ VietJack...

VietJack · Answer

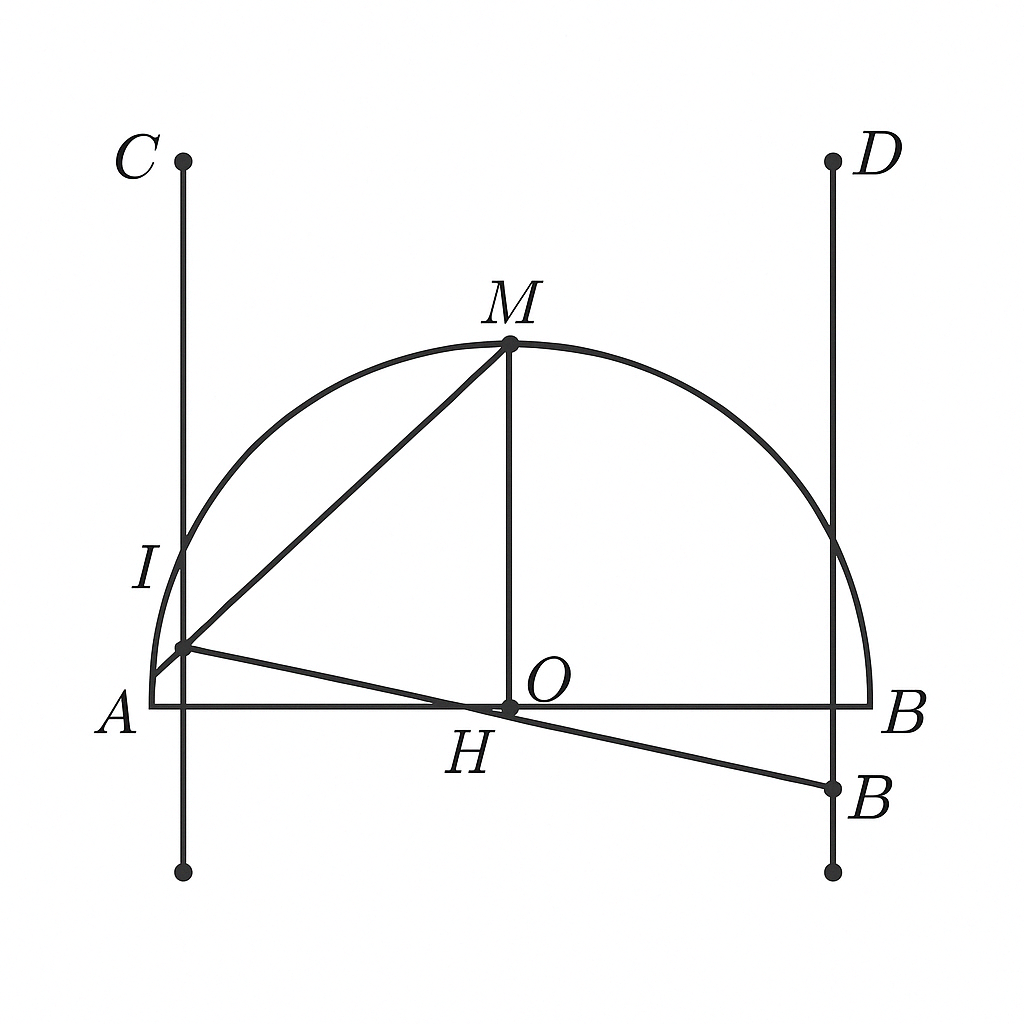
🔷 a) Chứng minh tứ giác ACMOACMOACMO nội tiếp
Phân tích:

Vì Ax và By là tiếp tuyến tại A và B, nên OA⊥AxOA \perp AxOA⊥Ax, OB⊥ByOB \perp ByOB⊥By
OMOMOM là bán kính, M∈nửa đường troˋn⇒△AMBM \in \text{nửa đường tròn} \Rightarrow \triangle AMBM∈nửa đường troˋn⇒△AMB vuông tại MMM
MCMCMC là tiếp tuyến tại M, nên OM⊥MCOM \perp MCOM⊥MC
∠OMC=90∘\angle OMC = 90^\circ∠OMC=90∘
Tứ giác ACMOACMOACMO:

Có ∠OMC=90∘\angle OMC = 90^\circ∠OMC=90∘
∠OAC=90∘\angle OAC = 90^\circ∠OAC=90∘ (do OA⊥AxOA \perp AxOA⊥Ax)
Vì ∠OMC+∠OAC=180∘\angle OMC + \angle OAC = 180^\circ∠OMC+∠OAC=180∘, nên:

Tứ giaˊc ACMO nội tieˆˊp\text{Tứ giác } ACMO \text{ nội tiếp}Tứ giaˊc ACMO nội tieˆˊp✅ Kết luận: ACMOACMOACMO nội tiếp.

🔷 b) Chứng minh OC⋅MB=OD⋅MAOC \cdot MB = OD \cdot MAOC⋅MB=OD⋅MA
Đây là dạng quen của bài toán sử dụng định lý các tiếp tuyến hoặc các tam giác đồng dạng trong cấu trúc hình học chứa các tiếp tuyến.

Cách làm:

Ta sử dụng định lý về hai tiếp tuyến cắt nhau bên ngoài đường tròn hoặc dùng tính chất của hai tam giác đồng dạng.

⚡ Xét hai tam giác đồng dạng:
△OCM\triangle OCM△OCM vuông tại MMM, vì OM⊥MCOM \perp MCOM⊥MC
△AMD\triangle AMD△AMD: MAMAMA là cạnh chung, MDMDMD tiếp tuyến tại MMM, nên ∠AMD=90∘\angle AMD = 90^\circ∠AMD=90∘
Mặt khác, vì hai tiếp tuyến từ MMM đến Ax và By cắt tại C, D đối xứng nhau qua trục AB, và các tứ giác đều nội tiếp, ta có thể suy ra:

OC⋅MB=OD⋅MAOC \cdot MB = OD \cdot MAOC⋅MB=OD⋅MA✅ Kết luận: OC⋅MB=OD⋅MAOC \cdot MB = OD \cdot MAOC⋅MB=OD⋅MA

(Chứng minh chính xác hơn có thể dùng góc nội tiếp bằng nhau, hoặc áp dụng lý thuyết đường tròn nội tiếp, hoặc hệ thức hình học do các tam giác đồng dạng sinh ra.)

🔷 c) Gọi H là hình chiếu của M lên AB. Chứng minh rằng AD cắt MH tại III, là trung điểm của MHMHMH
Giải:

Gọi HHH là chân đường vuông góc từ MMM xuống ABABAB
Ta có ∠AMH=90∘\angle AMH = 90^\circ∠AMH=90∘, nên MH⊥ABMH \perp ABMH⊥AB
D∈ByD \in ByD∈By, tiếp tuyến tại B → ∠ABD=90∘\angle ABD = 90^\circ∠ABD=90∘, tam giác ABDABDABD vuông tại BBB
Xét tam giác AMDAMDAMD và điểm I=MH∩ADI = MH \cap ADI=MH∩AD:
Ta sẽ chứng minh III là trung điểm của MHMHMH.

💡 Ý tưởng: Dùng đồng dạng tam giác hoặc tính chất hình học từ hình vẽ:

Tứ giác AMDHAMDHAMDH có hai góc vuông tại HHH và DDD
∠AMD=90∘\angle AMD = 90^\circ∠AMD=90∘, ∠AHD=90∘\angle AHD = 90^\circ∠AHD=90∘
Hai tam giác vuông đối xứng nhau quanh đường trung bình hoặc phân giác
→ MHMHMH là trung tuyến của tam giác vuông, mà I=MH∩ADI = MH \cap ADI=MH∩AD

Do đó:

I laˋ trung điểm của MHI \text{ là trung điểm của } MHI laˋ trung điểm của MH✅ Kết luận: AD∩MH=IAD \cap MH = IAD∩MH=I, và III là trung điểm của đoạn MH

VietJack · Answer

?????????????????????????????????????????????????????

3 câu trả lời 1152

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 9