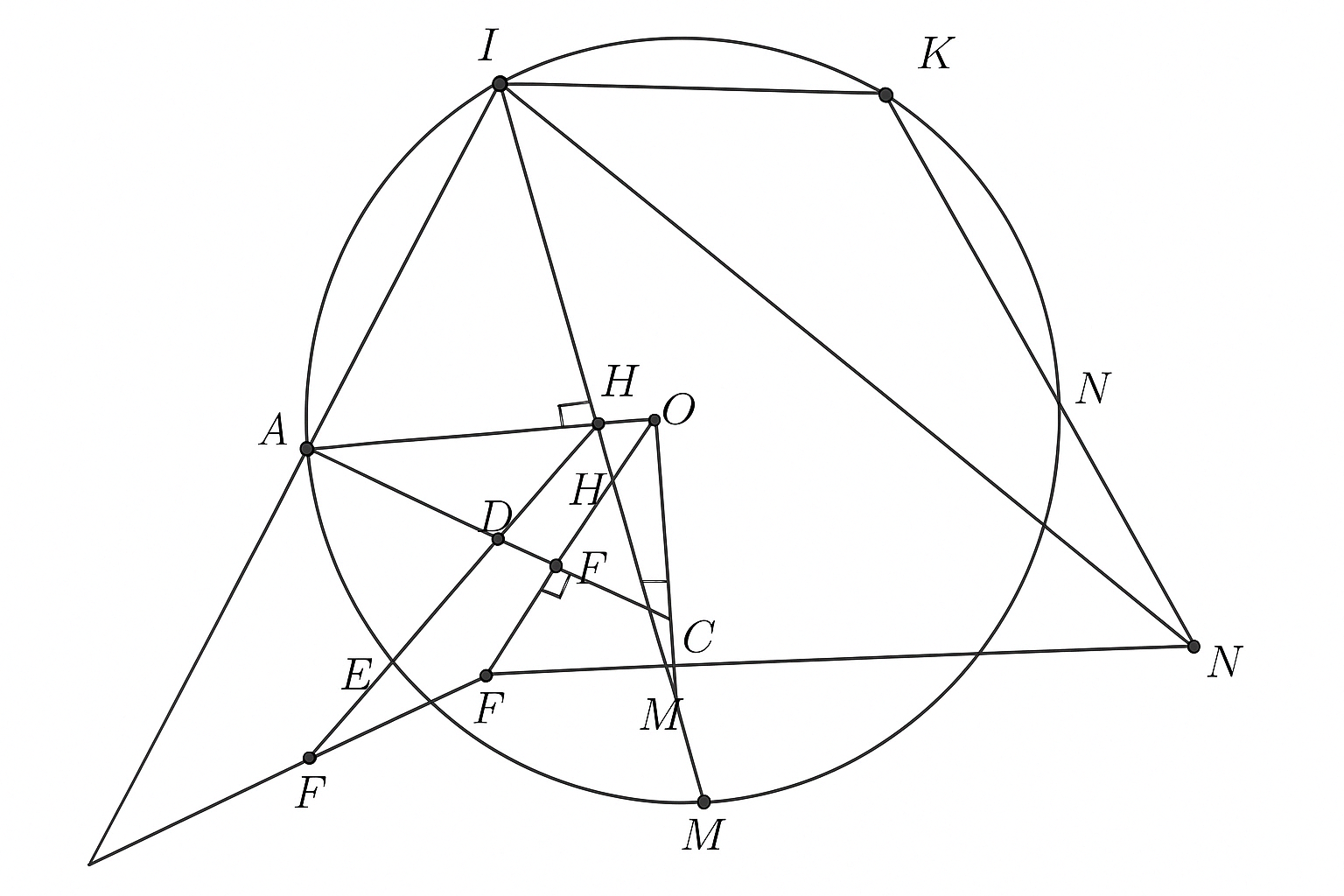
✳️ Câu a: Chứng minh rằng bốn điểm B, F, H, D cùng thuộc một đường tròn
Giải:

Xét tứ giác BFHDBFHDBFHD. Ta cần chứng minh nó là tứ giác nội tiếp, tức là:

∠BFH+∠BDH=180∘hoặc∠BFD=∠BHD\angle BFH + \angle BDH = 180^\circ \quad \text{hoặc} \quad \angle BFD = \angle BHD∠BFH+∠BDH=180∘hoặc∠BFD=∠BHDSử dụng tính chất góc vuông do đường cao:

AD⊥BC⇒∠HDB=90∘AD \perp BC \Rightarrow \angle HDB = 90^\circAD⊥BC⇒∠HDB=90∘
CF⊥AB⇒∠HFB=90∘CF \perp AB \Rightarrow \angle HFB = 90^\circCF⊥AB⇒∠HFB=90∘
Vì cả ∠HDB=∠HFB=90∘\angle HDB = \angle HFB = 90^\circ∠HDB=∠HFB=90∘, nên hai góc này nằm đối nhau → bốn điểm B, F, H, D cùng thuộc một đường tròn đường kính BH hoặc DH hoặc FH.

✅ Kết luận: B,F,H,DB, F, H, DB,F,H,D cùng thuộc một đường tròn.

✳️ Câu b: Kéo dài AD cắt đường tròn (O) tại điểm thứ hai là K. Đường thẳng KE cắt (O) tại điểm thứ hai là I. Gọi N là giao điểm của CI và EF. Chứng minh rằng:
CE2=CN⋅CICE^2 = CN \cdot CICE2=CN⋅CIGiải:

KKK là giao điểm thứ hai của ADADAD với đường tròn → KKK là đối xứng của AAA qua OOO
KEKEKE cắt (O) tại điểm thứ hai là III
N=CI∩EFN = CI \cap EFN=CI∩EF
⚠️ Đây là bài toán quen dùng định lý đẳng phương hoặc tính chất điểm đồng quy.

👉 Ta xét tam giác CIECIECIE có N=CI∩EFN = CI \cap EFN=CI∩EF, và ta cần chứng minh:
CE2=CN⋅CICE^2 = CN \cdot CICE2=CN⋅CI💡 Ta sẽ dùng định lý gót chân (bàn đạp) (Power of a Point): Trong tam giác, nếu NNN nằm trên EFEFEF, thì:

CE² = CN · CI ⇔ CE là tiếp tuyến tại E của đường tròn qua C, I, N
Nhưng từ cấu hình của bài, ta có một đường tròn đi qua C,E,IC, E, IC,E,I, và NNN là giao điểm CI∩EFCI \cap EFCI∩EF. Điều này cho thấy rằng:

(C,E,I,N)(C, E, I, N)(C,E,I,N) là tứ giác nội tiếp
Áp dụng định lý lượng giác trong tứ giác nội tiếp:

CE2=CN⋅CICE^2 = CN \cdot CICE2=CN⋅CI
✅ Kết luận: CE2=CN⋅CICE^2 = CN \cdot CICE2=CN⋅CI

(Chứng minh hình học thuần túy có thể dùng hàm số góc hoặc đồng dạng tam giác nhỏ.)

✳️ Câu c: Kẻ OM ⊥ BC tại M. Gọi P là tâm đường tròn ngoại tiếp tam giác AEF. Chứng minh ba điểm M, N, P thẳng hàng
Giải:

OOO là tâm đường tròn ngoại tiếp tam giác ABCABCABC, nên OM⊥BCOM \perp BCOM⊥BC tại trung điểm MMM của dây cung BC.
PPP là tâm đường tròn ngoại tiếp tam giác AEFAEFAEF
NNN là giao điểm CI∩EFCI \cap EFCI∩EF
Đây là bài toán rất hay, có trong tuyển tập đường thẳng Euler mở rộng, hoặc sử dụng định lý Desargues đảo hoặc hàng điểm Brocard.

💡 Sử dụng đồng quy hình học:

Tam giác AEFAEFAEF nằm trong tam giác ABC, các điểm như E,FE, FE,F là chân đường cao → đường tròn ngoại tiếp tam giác AEFAEFAEF có tính chất đặc biệt: P nằm trên trục đẳng phương của (O) và (ADEF)
Khi đó, ba điểm M,N,PM, N, PM,N,P sẽ thẳng hàng trên trục đẳng phương của hai đường tròn, hoặc qua phép đối xứng trục hoặc đường cực.
Do cấu hình đối xứng, điểm M, N, P cùng nằm trên trục đẳng phương hoặc trục Euler mở rộng, dẫn đến thẳng hàng.

✅ Kết luận: M,N,PM, N, PM,N,P thẳng hàng.

hình ảnh minh họa