Cho ABC cân tại A . Gọi H là trung điểm của BC
A)Chứng minh :ABH = ACH
B) Vẽ HM,HN lần lượt vuông góc với AB , AC tại M và N . Chứng minh AMN cân
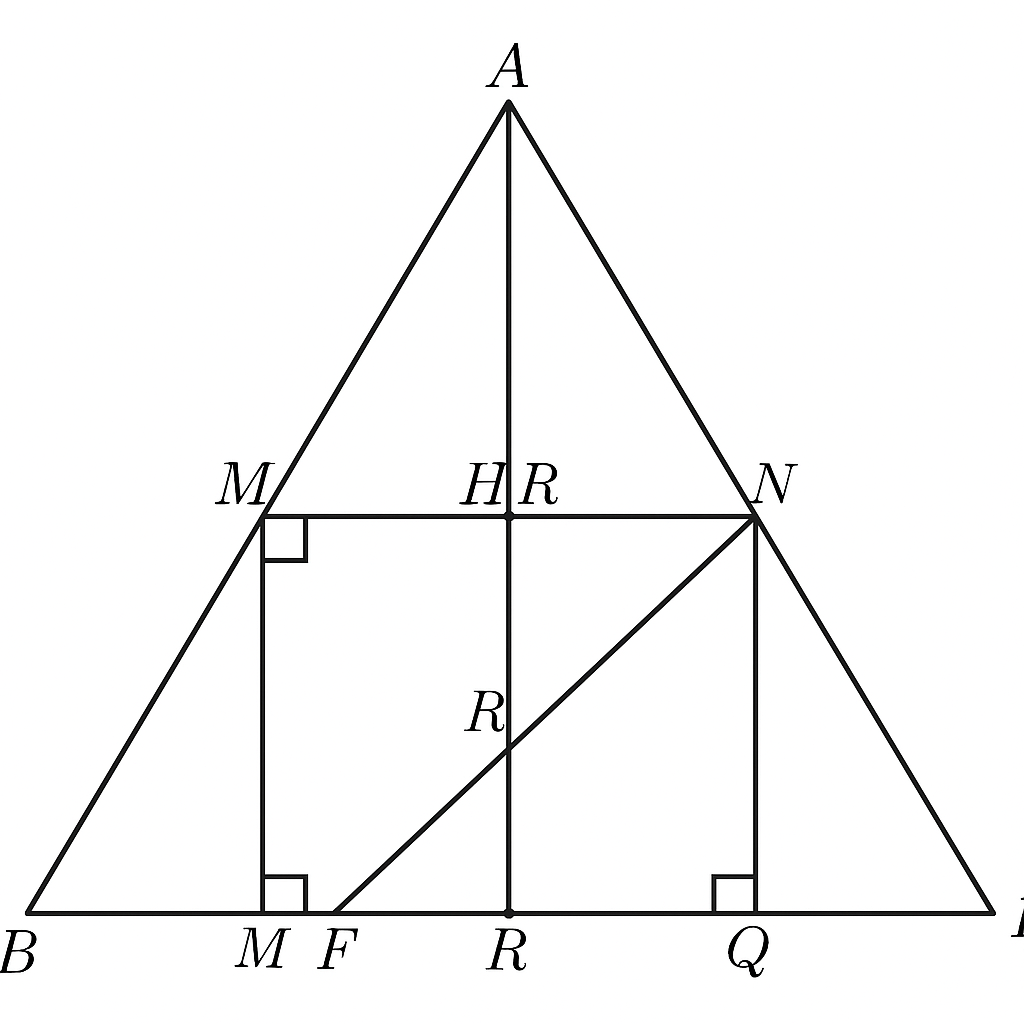
C) Trên tia đối của tia NH lấy điểm E sao cho NE=NH . Gọi F là trung điểm của MH . Gọi R,Q lần lượt là giao điểm của AH , EF với MN . Chứng minh : MN = RQ
Quảng cáo
1 câu trả lời 857
A) Chứng minh: ΔABH = ΔACH
- Tam giác ABC cân tại A ⇒ AB = AC
- H là trung điểm của BC ⇒ BH = CH
- Góc chung: ∠AHB = ∠AHC
⇒ ΔABH = ΔACH (c.g.c)
B) Vẽ HM ⊥ AB tại M, HN ⊥ AC tại N. Chứng minh ΔAMN cân
Xét tam giác AMN:
- HM ⊥ AB ⇒ góc HMB = 90°
- HN ⊥ AC ⇒ góc HNC = 90°
→ Hai đường vuông góc cùng xuất phát từ H
Mà tam giác ABC cân tại A ⇒ hai cạnh AB = AC
⇒ Hai đường vuông góc từ H đến AB và AC đối xứng nhau
⇒ HM = HN (do đối xứng)
⇒ KM và N cũng đối xứng nhau qua đường phân giác của góc A
⇒ Tam giác AMN có AM = AN
=> ΔAMN cân tại A
C) Trên tia đối của NH lấy điểm E sao cho NE = NH
- F là trung điểm của MH
- AH cắt MN tại R
- EF cắt MN tại Q
→ Chứng minh: MN = RQ
- Vì NE = NH, nên điểm E đối xứng H qua điểm N
→ Tam giác HEN cân tại N
- F là trung điểm của MH
→ EF là đoạn nối từ trung điểm MH đến đối xứng của H (qua N)
→ Vì tam giác AMN cân, AH là đường trung tuyến (vì tam giác cân tại A) nên:
→ AH ⊥ MN tại R
→ EF ⊥ MN tại Q (do tính chất đối xứng và trung điểm)
AH và EF cùng vuông góc với MN tại R và Q
→ R và Q cách đều hai đầu M và N
⇒ MN = RQ
- a) ΔABH = ΔACH
- b) ΔAMN cân tại A
- c) MN = RQ
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
12233
-
5721
-
4825


