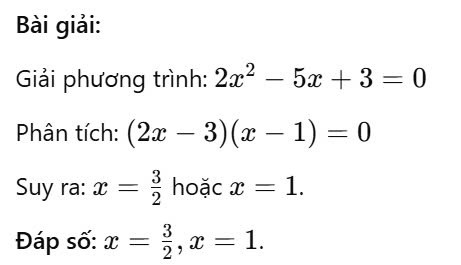Quảng cáo
2 câu trả lời 244
Biểu thức bạn cung cấp là \(2x^2 - 5x + 3\). Đây là một đa thức bậc hai, và chúng ta có thể phân tích hoặc giải phương trình bằng cách sử dụng công thức nghiệm của phương trình bậc hai.
Để giải phương trình bậc hai \(2x^2 - 5x + 3 = 0\), chúng ta có thể sử dụng công thức nghiệm:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Trong trường hợp này, \(a = 2\), \(b = -5\), và \(c = 3\). Bây giờ hãy tính các giá trị:
1. Tính \(\Delta\) (định thức):
\[
\Delta = b^2 - 4ac = (-5)^2 - 4 \cdot 2 \cdot 3 = 25 - 24 = 1
\]
2. Sử dụng công thức nghiệm:
\[
x = \frac{-(-5) \pm \sqrt{1}}{2 \cdot 2} = \frac{5 \pm 1}{4}
\]
3. Tính hai nghiệm:
- Nghiệm 1:
\[
x_1 = \frac{5 + 1}{4} = \frac{6}{4} = \frac{3}{2}
\]
- Nghiệm 2:
\[
x_2 = \frac{5 - 1}{4} = \frac{4}{4} = 1
\]
Vậy, phương trình \(2x^2 - 5x + 3 = 0\) có hai nghiệm: \(x = \frac{3}{2}\) và \(x = 1\).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4934
