Giải bất phương trình: x2 + 2x + 2 > 0
Quảng cáo
2 câu trả lời 355
Đặt y = x2 + 2x + 2.
Ta vẽ đồ thị hàm số bậc hai trên.
Ta có: a = 1, b = 2, c = 2 và ∆ = 22 – 4 . 1 . 2 = – 4 < 0.
- Tọa độ đỉnh I(– 1; 1).
- Trục đối xứng x = – 1.
- Giao điểm của parabol với trục tung là A(0; 2).
- Parabol không cắt trục hoành.
- Điểm đối xứng với điểm A(0; 2) qua trục đối xứng x = – 1 là B(– 2; 2).
Do a = 1 > 0 nên bề lõm của đồ thị hướng lên trên.
Ta có đồ thị hàm số y = x2 + 2x + 2 như hình dưới:
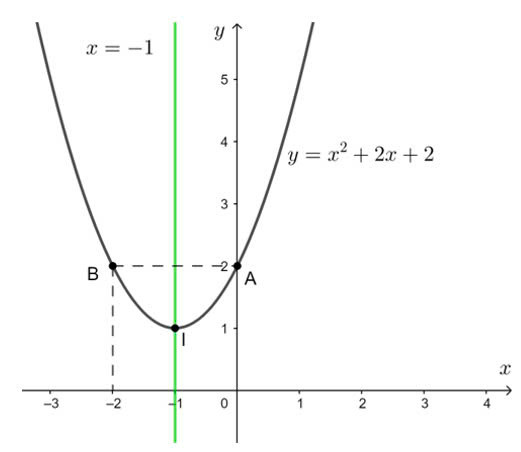
Quan sát đồ thị trên, ta thấy: x2 + 2x + 2 > 0 biểu diễn phần parabol y = x2 + 2x + 2 nằm phía trên trục hoành, tương ứng với mọi x
Vậy tập nghiệm của bất phương trình x2 + 2x + 2 > 0 là mọi x
Ta có (x + 1)2 > 0 (luôn đúng)
Vậy bất phương trình luôn đúng với mọi x
chúc bạn học tốt
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
12623
-
11326
-
9436
-
5628


