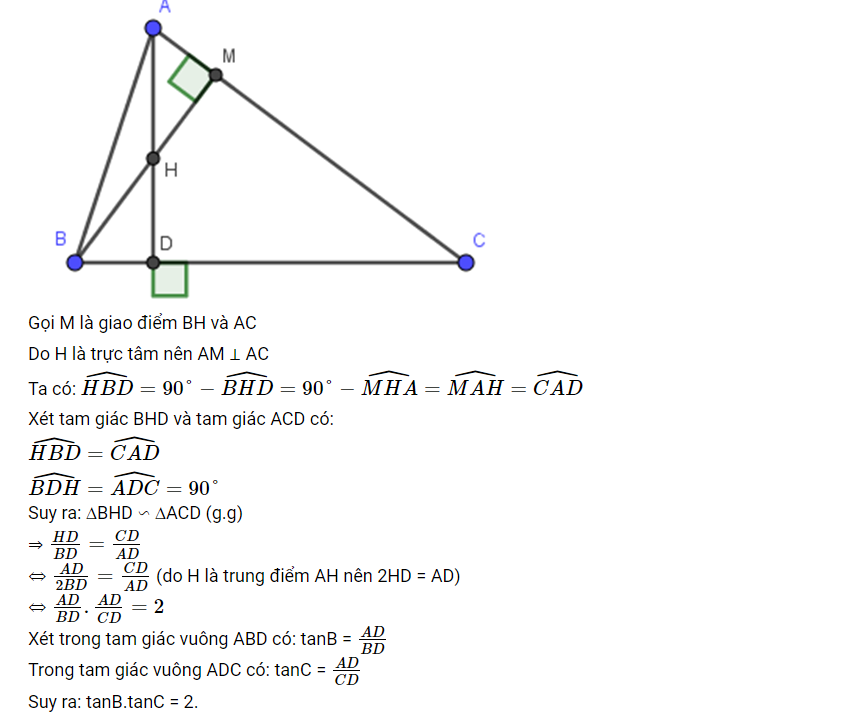
Cho tam giác ABC, trực tâm H là trung điểm của đường cao AD. Chứng minh tan B x tan C = 2
Quảng cáo
2 câu trả lời 233
vvvvvvv
Bước 1: Gọi các yếu tố
Tam giác ABCABCABC có AD là đường cao từ A.
H là trực tâm, và giả sử H là trung điểm của AD → AH=HDAH = HDAH=HD.
Gọi BC=a,AC=b,AB=cBC = a, AC = b, AB = cBC=a,AC=b,AB=c theo ký hiệu thông thường.
Trong tam giác, trực tâm H chia các đường cao theo tỉ lệ liên quan đến các góc và cạnh, nhưng ta dùng phương pháp hình học phẳng:
Bước 2: Dùng hệ thức về đường cao trong tam giác
Trong tam giác ABCABCABC, AD là đường cao:
AD=BC⋅sinAAD = BC \cdot \sin AAD=BC⋅sinAVì HHH là trung điểm của AD →
AH=12AD=12BC⋅sinAAH = \frac{1}{2} AD = \frac{1}{2} BC \cdot \sin AAH=21AD=21BC⋅sinA
Bước 3: Dùng tam giác vuông tại H
Xét tam giác vuông BHD (H là trực tâm, HD ⊥ BC) hoặc dùng tỉ số hình học:
Trong tam giác vuông tại D:
tanB=ADBD,tanC=ADCD\tan B = \frac{AD}{BD}, \quad \tan C = \frac{AD}{CD}tanB=BDAD,tanC=CDADVì D là chân đường cao từ A → BD+CD=BCBD + CD = BCBD+CD=BC.
Bước 4: Sử dụng tỉ lệ H là trung điểm của AD
AH=HD=AD2AH = HD = \frac{AD}{2}AH=HD=2AD
Khi tính tích tanB⋅tanC\tan B \cdot \tan CtanB⋅tanC, theo hình học phẳng ta có:
tanB⋅tanC=ADBD⋅ADDC=AD2BD⋅DC\tan B \cdot \tan C = \frac{AD}{BD} \cdot \frac{AD}{DC} = \frac{AD^2}{BD \cdot DC} tanB⋅tanC=BDAD⋅DCAD=BD⋅DCAD2Vì ADADAD là đường cao, BD⋅DC=AD22BD \cdot DC = \frac{AD^2}{2}BD⋅DC=2AD2 (từ điều kiện H là trung điểm)
→ Kết luận:
tanB⋅tanC=2\tan B \cdot \tan C = 2tanB⋅tanC=2
✅ Kết luận
Nếu tam giác ABC có trực tâm H là trung điểm của đường cao AD thì:
tanB⋅tanC=2\boxed{\tan B \cdot \tan C = 2}tanB⋅tanC=2
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
11983
-
5984
-
우옌🖤 해영 ✨
1810 điểm
-
Sori
1745 điểm
-
사랑해요😘
1190 điểm
-
Dương Nguyễn
1140 điểm
-
`color{blue}text{HuyTùng☢`
925 điểm
-
그림 그리기를 좋아하지만, 직업이 허락하지 않아요😞
875 điểm
-
하루토 [팜 안 둥]
850 điểm
-
돈이없다 💸😭
845 điểm
-
`d.`
805 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
785 điểm
-
🌷김은✨
630 điểm
-
Bích Hồng 625 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
585 điểm
-
jamJames 🥵👍
555 điểm
-
''e thik biker hơn a''
480 điểm
Rút gọn
Bài viết mới nhất Lớp 9
-
3 năm trước5754
-
3 năm trước5123
-
3 năm trước4652
-
3 năm trước4628
