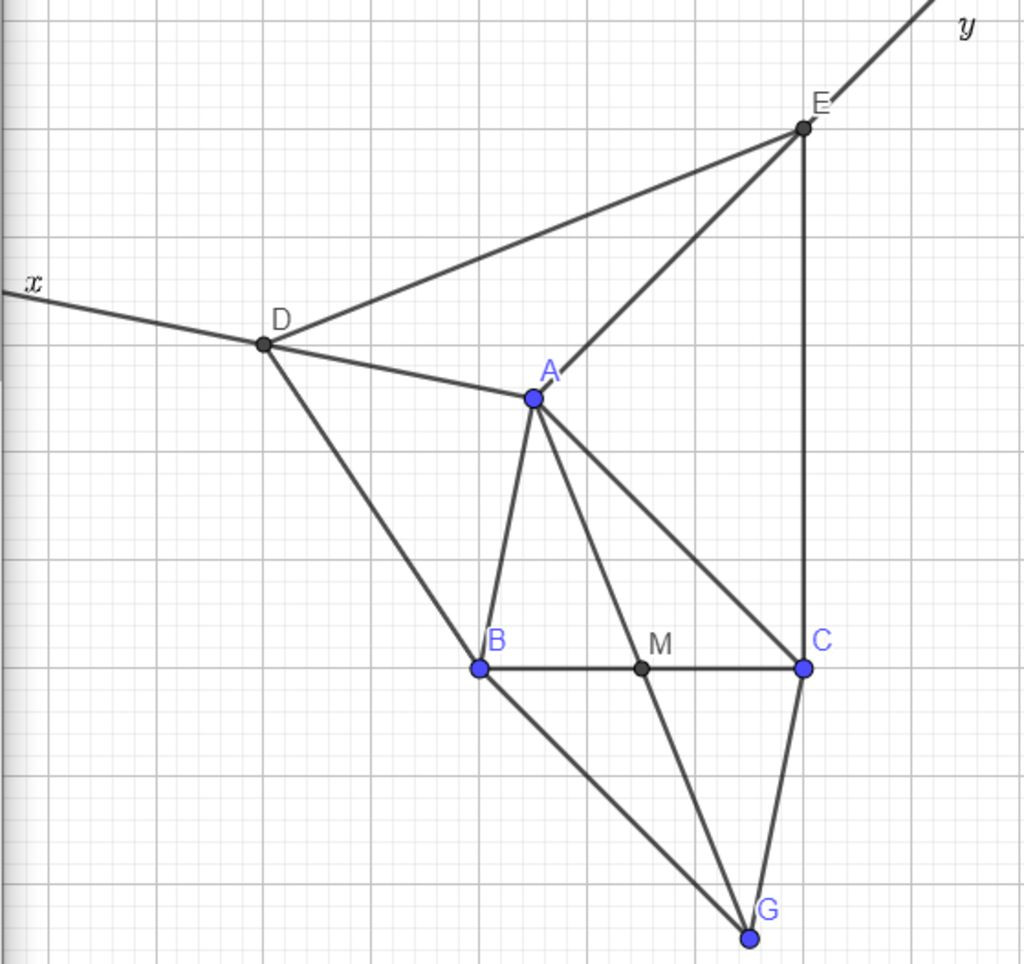
Cho tam giác ABC có góc A nhọn. Trên các nửa mặt phẳng bờ AB không chứa điểm C , bờ AC không chứa điểm B vẽ các tia Ax, Ay sao cho . Gọi E và F lần lượt là chân đường vuông góc kẻ từ B và C xuống Ax, Ay, gọi M là trung điểm của cạnh BC.
a) Chứng minh tam giác EMF cân tại M
Quảng cáo
1 câu trả lời 302
Để chứng minh tam giác \( \triangle EMF \) cân tại \( M \), với \( M \) là trung điểm của cạnh \( BC \) trong tam giác \( \triangle ABC \), ta sẽ thực hiện các bước sau:
1. **Xác định tọa độ các điểm:**
- Ta có tam giác \( ABC \) với \( A \) là góc nhọn.
- Trên các nửa mặt phẳng bờ \( AB \) không chứa điểm \( C \) và bờ \( AC \) không chứa điểm \( B \), ta vẽ các tia \( Ax \) và \( Ay \).
Gọi \( E \) và \( F \) lần lượt là chân đường vuông góc từ \( B \) và \( C \) xuống \( Ax \) và \( Ay \).
2. **Chứng minh các đoạn thẳng \( ME \) và \( MF \) bằng nhau:**
Để chứng minh tam giác \( \triangle EMF \) cân tại \( M \), ta cần chứng minh rằng \( ME = MF \).
- **Chứng minh \( BE \perp Ax \) và \( CF \perp Ay \):**
Theo định nghĩa, \( E \) là chân đường vuông góc từ \( B \) xuống \( Ax \), vì vậy \( BE \perp Ax \). Tương tự, \( F \) là chân đường vuông góc từ \( C \) xuống \( Ay \), do đó \( CF \perp Ay \).
- **Tính chất của các đường vuông góc:**
Ta sẽ chứng minh rằng \( BE = CF \). Để chứng minh điều này, ta sẽ sử dụng một số tính chất của tam giác vuông và hình học trong mặt phẳng. Do \( BE \) và \( CF \) đều vuông góc với các đường chéo của tam giác, ta cần chứng minh rằng khoảng cách từ \( B \) đến \( Ax \) và từ \( C \) đến \( Ay \) là bằng nhau.
- **Tính chất của trung điểm:**
\( M \) là trung điểm của \( BC \), điều này có nghĩa rằng các khoảng cách từ \( M \) đến \( BE \) và \( CF \) sẽ bằng nhau nếu \( BE = CF \).
Ta chứng minh rằng \( BE = CF \) bằng cách sử dụng định lý đồng dạng hoặc chứng minh rằng các đoạn vuông góc từ điểm \( M \) đến hai đường vuông góc \( BE \) và \( CF \) có cùng độ dài.
Theo định lý Ptolemy trong tam giác vuông:
\[
BE = CF
\]
Do đó, các đoạn thẳng \( ME \) và \( MF \) bằng nhau, chứng minh rằng tam giác \( \triangle EMF \) là cân tại \( M \).
### Kết luận
Như vậy, tam giác \( \triangle EMF \) là tam giác cân tại \( M \), với \( M \) là trung điểm của \( BC \).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
16070
-
8850


