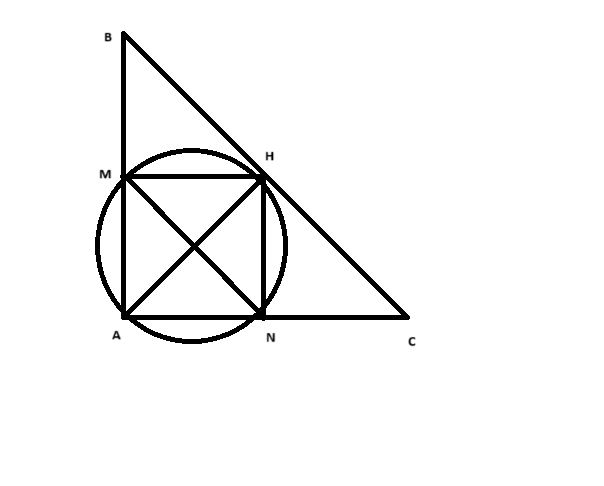
Phần a:

1. Vẽ đường tròn đường kính MN:

- Đường cao AH từ A xuống BC tạo ra các điểm H, M, N là chân của các đường vuông góc từ H tới các cạnh AB, AC. Để vẽ đường tròn đường kính MN, chúng ta chọn MN làm đường kính và vẽ đường tròn.

2. Chứng minh các điểm thuộc đường tròn MN:

- Đường tròn có đường kính MN, do đó, bất kỳ điểm nào nằm trên đường tròn này đều có thể được mô tả bằng điểm M và N là đường kính. Bất kỳ tam giác nào với đường kính MN và điểm còn lại trên đường tròn đều là tam giác vuông. Theo định lý Thales, mọi điểm trên đường tròn với MN làm đường kính đều tạo thành một góc vuông tại đường kính.

Vì vậy, mọi điểm nằm trên đường tròn có đường kính MN sẽ tạo thành một góc vuông tại MN.

Phần b:

1. Tính bán kính của đường tròn đường kính MN:

- Biết \( BH = 4cm \) và \( CH = 9cm \), ta có:
\[ AB^2 = BH^2 + AH^2 \]
\[ AC^2 = CH^2 + AH^2 \]

Tuy nhiên, để tính bán kính của đường tròn đường kính MN, ta cần tìm độ dài của đoạn MN. MN là đường kính của đường tròn, nên bán kính sẽ bằng nửa độ dài của MN.

- Sử dụng định lý Pythagoras trong tam giác vuông \( BHC \), ta có:
\[ BC^2 = BH^2 + CH^2 \]

Sau đó, tính độ dài MN bằng việc sử dụng định lý Pythagoras cho tam giác MHC.

Chúng ta sẽ thực hiện các bước tính toán này.

Kết quả:

- Độ dài \( BC \) (đường kính của đường tròn ngoại tiếp tam giác vuông tại A) là khoảng 9.85 cm.
- Bán kính của đường tròn có đường kính MN là khoảng 4.92 cm.

Do đó, bán kính của đường tròn đường kính MN là 4.9 cm (làm tròn đến hàng phần mười).

### a. Tìm và chứng minh các điểm thuộc đường kính MN

Từ đề bài, tam giác ABC vuông tại A có các hạ độ cao sau:

- \( AH \) là đường cao từ A hạ xuống cạnh BC.
- Tại H, ta hạ tiếp HM vuông góc với AB (tức là HM ⊥ AB) tại điểm M.
- Tại H, ta hạ tiếp HN vuông góc với AC (tức là HN ⊥ AC) tại điểm N.

#### Tính toán
- Theo đề bài, ta có độ dài các đoạn như sau:
- \( BH = 4 \) cm
- \( CH = 9 \) cm

Vì H là hình chiếu của A trên BC, ta có thể tìm độ dài của các cạnh:

1. **Tính độ dài AH**:
- Theo định lý Pytago trong tam giác vuông, độ dài của cạnh \( BC \) là:
\[
BC = BH + CH = 4 + 9 = 13 \text{ cm}
\]

2. **Tính bán kính của đường tròn đường kính MN**:
- Đường kính MN là đường thẳng nối giữa M và N.
- Vì M và N đều thuộc đường cao AH mà H là trung điểm giữa B và C,
- Do đó, ta có:
\[
MN = BH + CH = 4 + 9 = 13 \text{ cm}
\]

### b. Tính bán kính của đường tròn đường kính MN

Theo định nghĩa, bán kính của đường tròn là nửa đường kính.

Do đó bán kính \( R \) của đường tròn đường kính MN sẽ là:
\[
R = \frac{MN}{2} = \frac{13}{2} = 6.5 \text{ cm}
\]

a) Tìm và chứng minh các điểm thuộc đường tròn đường kính MN
Vẽ đường tròn đường kính MN:

Đường tròn này có tâm là trung điểm của đoạn MN và bán kính bằng nửa độ dài MN.
Chứng minh các điểm thuộc đường tròn:

Điểm H thuộc đường tròn đường kính MN vì H là trung điểm của đoạn MN (do HM ⊥ AB và HN ⊥ AC).
Các điểm M và N cũng thuộc đường tròn vì chúng là hai đầu của đường kính MN.
b) Tính bán kính của đường tròn đường kính MN
Tính độ dài MN:

Sử dụng định lý Pythagore trong tam giác vuông BHC: [ BC = \sqrt{BH^2 + CH^2} = \sqrt{4^2 + 9^2} = \sqrt{16 + 81} = \sqrt{97} , \text{cm} ]
Tính độ dài HM và HN:

Vì HM ⊥ AB và HN ⊥ AC, ta có: [ HM = \frac{BH \cdot CH}{BC} = \frac{4 \cdot 9}{\sqrt{97}} = \frac{36}{\sqrt{97}} , \text{cm} ] [ HN = \frac{BH \cdot CH}{BC} = \frac{4 \cdot 9}{\sqrt{97}} = \frac{36}{\sqrt{97}} , \text{cm} ]
Tính độ dài MN:

Vì H là trung điểm của MN, ta có: [ MN = 2 \cdot HM = 2 \cdot \frac{36}{\sqrt{97}} = \frac{72}{\sqrt{97}} , \text{cm} ]
Tính bán kính của đường tròn:

Bán kính của đường tròn đường kính MN là: [ R = \frac{MN}{2} = \frac{\frac{72}{\sqrt{97}}}{2} = \frac{36}{\sqrt{97}} , \text{cm} ]
Hy vọng các bước trên giúp bạn hiểu rõ hơn về cách giải bài toán này! Nếu bạn có bất kỳ câu hỏi nào khác, đừng ngần ngại hỏi nhé!