Cho tam giác ABC có 3 góc nhọn, kẻ hai đường cao BD và CE cắt nhau tại H.
1, Chứng minh bốn điểm A, E, H, D cùng thuộc một đường tròn . xác định tâm I của đường tròn đó. 2, Chứng minh AH vuông góc BC. 3, Cho góc A = 600, AB = 6cm. tính BD.
4, Gọi O là trung điểm của BC. Chứng minh OD là tiếp tuyến của đường tròn (I
Quảng cáo
2 câu trả lời 10685
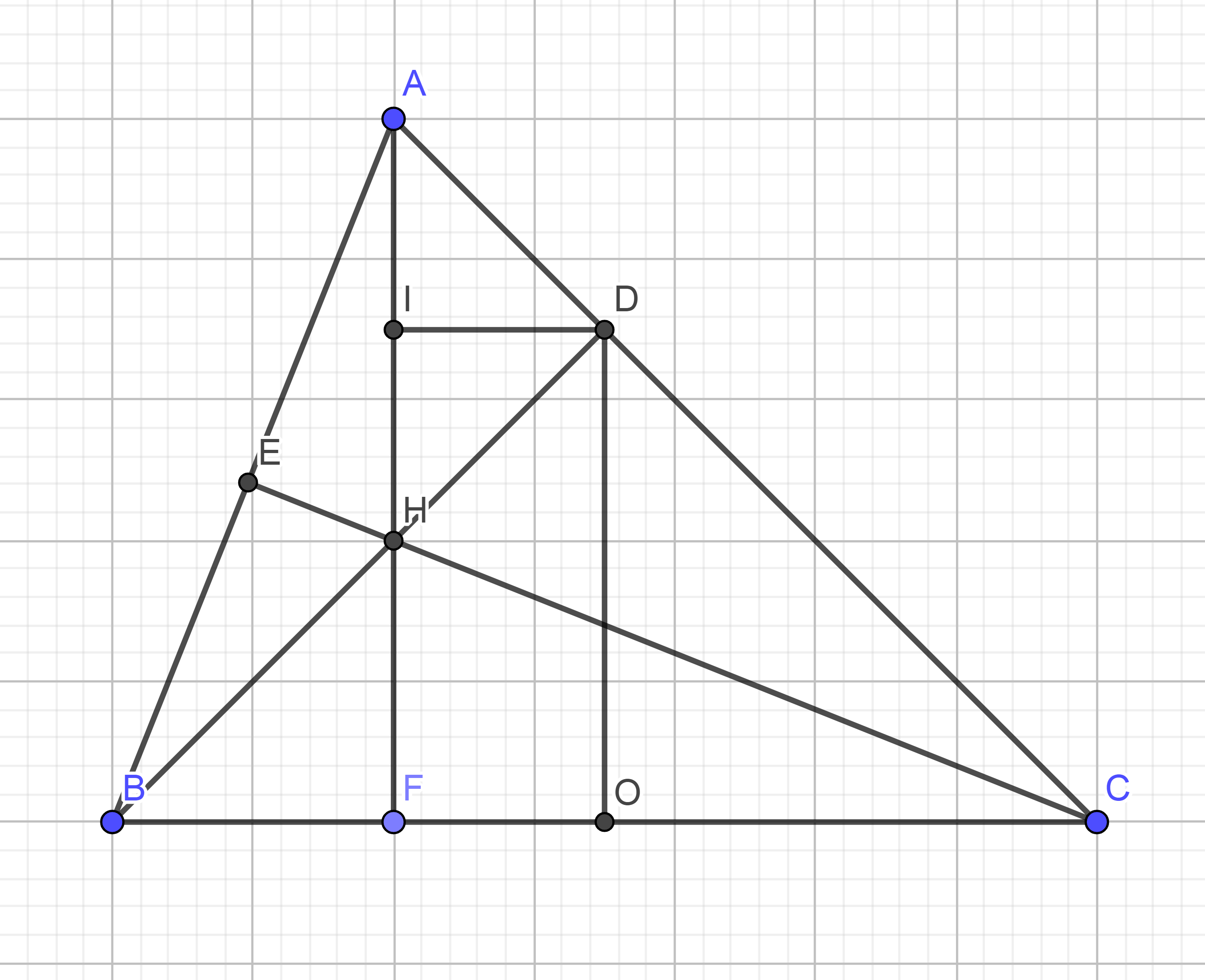
1) Xét tam giác ADH vuông tại D
=>A:D;H cùng thuộc đường tròn đường kính AH
Xét tam giác AEH vuông tại E
=>A:E;H cùng thuộc đường tròn đường kính AH
=>A:D;H;E cùng thuộc đường tròn đường kính AH
I là tâm đường tròn đó=> i là trung điểm của AH
2) Xét tam giác ABC có BD;CE là đường cao
BD cắt CE tại H
=> H là trực tâm của tam giác ABC
=>AH là đường cao thứ 3
=> AH vuông góc BC
3) Xét tam giác ABD vuông tại D
\(\begin{array}{l}
\sin \widehat A = \frac{{BD}}{{AB}}\\
= > \sin {60^ \circ } = \frac{{BD}}{6}\\
= > BD = 3\sqrt 3 (cm)
\end{array}\)
4) Gọi AH cắt BC tại F
=> AF vuông góc BC
Xét tam giác ADH và tam giác AFC có:
Góc ADH=góc AFC=90
Góc FAC chung
=>Tam giác ADH \( \sim \) tam giác AFC(g-g)
=> Góc AHD =góc ACF
Ta có: ID=IH
=> Tam giác IDH cân tại I
=>Góc IDH=góc IHD
Xét tam giác BDC vuông tại D có O là trung điểm BC
=> OD=OB=OC
=>Tam giác ODC cân tại O
=>Góc ODC=góc OCD
Tương tự ta có OBD=góc ODB
Có Góc BDO+góc ODC=90
=>góc IDH+góc BDO=90
=>góc IDO=90
=> ID vuông góc DO
Xét (I) có DO vuông góc ID tại D
=> DO là tiếp tuyến của (I) tại D.
Chứng minh bốn điểm A.E.H.D cùng thua một đường tròn xác định tâm I
của đường tròn đó
Quảng cáo
Câu hỏi hot cùng chủ đề
-
1 9361
Bài viết mới nhất Lớp 9
-
2 năm trước4342
-
2 năm trước3780
-
2 năm trước3571
-
2 năm trước3513
