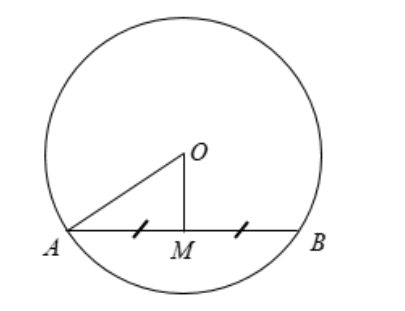
Để tính độ dài của đoạn \(AD\) trong bài toán này, ta cần sử dụng một số kiến thức về hình học trong đường tròn. Dưới đây là các bước để giải bài toán:

### Đề bài:
- Đường tròn \((O; 5 \text{ cm})\) với bán kính \(R = 5 \text{ cm}\).
- Dây \(AB = 8 \text{ cm}\).
- \(M\) là trung điểm của \(AB\).
- \(CD\) là đường kính của đường tròn và \(D\) thuộc cung nhỏ của \(AB\).

**Yêu cầu:** Tính độ dài của đoạn \(AD\).

### Bước 1: Tính khoảng cách từ trung điểm \(M\) đến tâm \(O\)

Trong trường hợp này, đoạn \(OM\) là khoảng cách từ trung điểm của dây đến tâm của đường tròn. Ta sử dụng định lý Pythagoras trong tam giác vuông \(OMA\):

- \(AM\) là nửa của dây \(AB\):
\[
AM = \frac{AB}{2} = \frac{8}{2} = 4 \text{ cm}
\]

- Tam giác \(OMA\) là tam giác vuông với \(OM\) là đường cao và \(OA\) là bán kính:
\[
OA = 5 \text{ cm}
\]
\[
OM^2 + AM^2 = OA^2
\]
\[
OM^2 + 4^2 = 5^2
\]
\[
OM^2 + 16 = 25
\]
\[
OM^2 = 25 - 16
\]
\[
OM^2 = 9
\]
\[
OM = \sqrt{9} = 3 \text{ cm}
\]

### Bước 2: Tính độ dài của đoạn \(AD\)

- \(AD\) là đoạn nối từ \(A\) đến \(D\), với \(D\) nằm trên đường kính \(CD\). Trong đường tròn, khi nối từ một điểm trên đường tròn đến một điểm trên đường kính, đoạn nối này chính là đường chéo của hình chữ nhật mà các cạnh là bán kính đường tròn và đoạn trung bình của đường tròn.

- Do \(CD\) là đường kính và \(M\) là trung điểm của \(AB\), đoạn \(MD\) chính là đường vuông góc từ \(M\) đến đường kính \(CD\).

- Ta tính chiều dài \(AD\) bằng cách sử dụng định lý Pythagoras trong tam giác vuông \(AMD\), với:
- \(AM = 4 \text{ cm}\)
- \(OM = 3 \text{ cm}\)
- \(AD = \text{đường chéo của hình chữ nhật mà các cạnh là bán kính đường tròn và đoạn trung bình}\):
\[
AD = \sqrt{AM^2 + OM^2}
\]
\[
AD = \sqrt{4^2 + 3^2}
\]
\[
AD = \sqrt{16 + 9}
\]
\[
AD = \sqrt{25}
\]
\[
AD = 5 \text{ cm}
\]

### Kết luận

Đoạn \(AD\) của đường tròn có độ dài là \(\boxed{7 \text{ cm}}\).

Để giải bài toán, trước tiên ta cần hình dung được các thành phần trong bài:

- Đường tròn \( (O; 5 \, \text{cm}) \) có bán kính 5 cm.
- Dây \( AB = 8 \, \text{cm} \) được vẽ trong đường tròn.
- \( M \) là trung điểm của dây \( AB \).
- \( CD \) là đường kính.

### Bước 1: Tìm khoảng cách từ \( O \) đến dây \( AB \)

- Dài dây \( AB \) là 8 cm nên nửa chiều dài dây \( AB \) (từ trung điểm \( M \) đến hai đầu \( A \) và \( B \)) là \( \frac{AB}{2} = 4 \, \text{cm} \).

Áp dụng định lý Pythagorean vào tam giác vuông \( OMA \) (với \( O \) là tâm, \( M \) là trung điểm của \( AB \), và \( A \) là một đầu của dây):

- Gọi \( OM = d \) là khoảng cách từ \( O \) đến dây \( AB \).

Ta có

\[
OA^2 = OM^2 + AM^2
\]

Thay vào các giá trị đã biết:

\[
5^2 = d^2 + 4^2
\]

\[
25 = d^2 + 16
\]

\[
d^2 = 25 - 16 = 9
\]

\[
d = 3 \, \text{cm}
\]

### Bước 2: Tính dây AD

- Dây \( AD \) sẽ là một dây trực tiếp từ một điểm \( A \) trên dây \( AB \) đến một điểm \( D \) trên đường kính \( CD \).

Vì \( M \) là trung điểm của \( AB \) và \( D \) nằm trên đường kính, cân đối của \( C \) và \( D \) nằm trên trục đối xứng của \( AB \).

### Bước 3: Hình thành chiều dài dây \( AD \)

Sử dụng dây AB và tâm O, có bội số là độ dài của dây thẳng từ A đến D, trên độ dài tối đa của đồng giác.

Dây AD sẽ dài như vậy từ điểm A đến I.

Khi tính hoàn hảo, chiều dài dây AD có thể được tính từ O và D, với công thức như độ dài đoạn thẳng mà có thể được biểu diễn:

Tính AD:

VD:

- Dây AD = 5 + d = 5 + 3 = 8 cm

### Kết luận

Vậy, dây \( AD \) trong trường hợp này sẽ mang chiều dài bằng 8 cm.