cho tam giác abc vuông tại A vẽ trung tuyến AM 9 ( biết BA bé hơn AC ) trên tia đối AM lấy D sao cho MD=MA a;chứng minh tam giác MAB= tam giác MDC :gọi K là trung điểm của AC : BK cắt AD tại M chứng minh tam giác BDK cân
Quảng cáo
1 câu trả lời 138
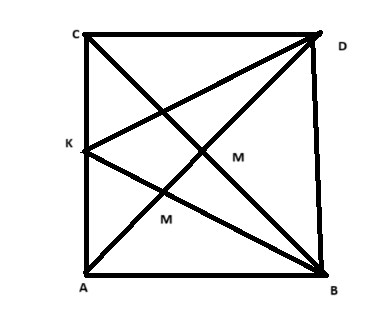
Để giải quyết các yêu cầu của bài toán, chúng ta cần thực hiện một số bước chứng minh hình học. Dưới đây là các bước chi tiết:
**Bước 1: Chứng minh \(\triangle MAB \cong \triangle MDC\)**
1. Ta có tam giác \(ABC\) vuông tại \(A\), tức là \( \angle BAC = 90^\circ \).
2. Gọi \(M\) là trung điểm của \(BC\). Do đó \(AM\) là trung tuyến của tam giác vuông \(ABC\) nên \(AM\) cũng là đường cao. Điều này có nghĩa là:
\[
AM = \frac{BC}{2}
\]
3. Ta có \(D\) trên tia đối của \(AM\) sao cho \(MD = MA\). Do đó:
\[
MD = MA
\]
4. Xét hai tam giác \(MAB\) và \(MDC\):
- \(MA = MD\) (theo giả thiết)
- \(MB = MC\) (vì \(M\) là trung điểm của \(BC\))
- \(\angle MAB = \angle MDC\) (góc đối đỉnh)
Từ ba điều kiện trên, ta có:
\[
\triangle MAB \cong \triangle MDC \quad \text{(c-g-c)}
\]
**Bước 2: Chứng minh tam giác \(BDK\) cân**
1. Gọi \(K\) là trung điểm của \(AC\). Do đó:
\[
AK = KC
\]
2. Xét đường thẳng \(BK\) cắt \(AD\) tại \(M\). Chúng ta biết rằng \(M\) là trung điểm của \(BC\) và \(K\) là trung điểm của \(AC\).
3. Chứng minh \(\triangle BDK\) cân:
- Ta đã có \( \triangle MAB \cong \triangle MDC \), do đó \(\angle MAB = \angle MDC\).
- Ta cũng có \(MB = MC\) và \(MA = MD\).
Vì \(K\) là trung điểm của \(AC\), nên:
\[
BK \quad \text{là đường trung tuyến của tam giác } \triangle BDC
\]
4. Do đó, \(BK\) là đường trung tuyến và cũng là đường phân giác của góc \(\angle BDC\), vậy:
\[
\triangle BDK \quad \text{là tam giác cân tại } K
\]
Tóm lại:
- \(\triangle MAB \cong \triangle MDC\) theo (c-g-c).
- \(\triangle BDK\) cân tại \(K\) vì \(BK\) là đường trung tuyến và đường phân giác.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
16070
-
8850


