cho tam giác ABC vuống tại A. Biết AB = 21cm, góc C =40 độ. tính độ dài AC, BC và tia phân giác AD
Quảng cáo
3 câu trả lời 815
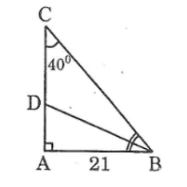
Ta có tam giác ABC vuông tại A, \( AB = 21 \) cm và \( \angle C = 40^\circ \).
**Bước 1: Tính độ dài AC và BC**
Vì tam giác ABC vuông tại A, ta sử dụng hàm sine để tính độ dài các cạnh:
Độ dài AC:
\[ AC = AB \cdot \sin(\angle C) \]
\[ AC = 21 \cdot \sin(40^\circ) \]
\[ AC \approx 21 \cdot 0.6428 \]
\[ AC \approx 13.50 \] cm (làm tròn đến hai chữ số thập phân)
Độ dài BC (là cạnh huyền của tam giác):
\[ BC = AB \cdot \cos(\angle C) \]
\[ BC = 21 \cdot \cos(40^\circ) \]
\[ BC \approx 21 \cdot 0.7660 \]
\[ BC \approx 16.09 \] cm (làm tròn đến hai chữ số thập phân)
Vậy:
\[ AC \approx 13.50 \] cm và \( BC \approx 16.09 \) cm.
**Bước 2: Tính độ dài tia phân giác AD**
Để tính độ dài tia phân giác AD, ta sử dụng định lý cosin trong tam giác vuông:
\[ AD = \sqrt{AB^2 + AC^2} \]
Đầu tiên, tính \( AB^2 \) và \( AC^2 \):
\[ AB^2 = 21^2 = 441 \]
\[ AC^2 \approx 13.50^2 \approx 182.25 \]
\[ AD = \sqrt{441 + 182.25} \]
\[ AD = \sqrt{623.25} \]
\[ AD \approx 24.98 \] cm (làm tròn đến hai chữ số thập phân)
Vậy, độ dài của tia phân giác AD là khoảng \( 24.98 \) cm.
**Kết luận:**
- Độ dài \( AC \approx 13.50 \) cm
- Độ dài \( BC \approx 16.09 \) cm
- Độ dài tia phân giác \( AD \approx 24.98 \) cm
Xét ΔABC vuông tại A có
tan C=AB/AC
=>21/AC=tan 40
=>𝐴𝐶≃25,03(𝑐𝑚)AC≃25,03(cm)
𝐵𝐶=𝐴𝐵2+𝐴𝐶2≃32,67(𝑐𝑚)BC=AB2+AC2≃32,67(cm)
mình nghe cô bảo là phải tính theo tính chất của tia phân giác 1 góc r áp dụng tính chất của dãy tỉ số bằng nhau á
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
16417
Đã trả lời bởi chuyên gia
16417 -
 Đã trả lời bởi chuyên gia
16377
Đã trả lời bởi chuyên gia
16377 -
 Đã trả lời bởi chuyên gia
15110
Đã trả lời bởi chuyên gia
15110 -
 Đã trả lời bởi chuyên gia
10151
Đã trả lời bởi chuyên gia
10151 -
 Đã trả lời bởi chuyên gia
7520
Đã trả lời bởi chuyên gia
7520


