Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của ˆBCD.
Quảng cáo
1 câu trả lời 393
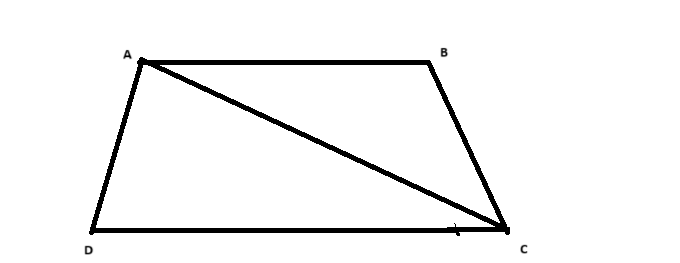
Để chứng minh \(CA\) là tia phân giác của góc \(\angle BCD\) trong hình thang cân \(ABCD\) với đáy nhỏ \(AB\) bằng cạnh bên \(BC\), ta thực hiện các bước sau:
Giả thiết:
- Hình thang cân \(ABCD\) có \(AB \parallel CD\), \(AB < CD\).
- \(AB = BC\).
Cần chứng minh:
- \(CA\) là tia phân giác của \(\angle BCD\).
Chứng minh:
1. Tính chất của hình thang cân:
- Hình thang cân \(ABCD\) có hai góc kề một đáy bằng nhau. Do đó, \(\angle DAB = \angle CDA\) và \(\angle ABC = \angle BCD\).
2. Định lý về tam giác cân:
- Trong tam giác \(ABC\), \(AB = BC\). Do đó, tam giác \(ABC\) là tam giác cân tại \(B\).
3. Tính chất đối xứng của hình thang cân:
- Do \(AB = BC\), nên \(\angle BAC = \angle BCA\).
4. Tam giác \(ACD\):
- Xét tam giác \(ACD\), ta có:
\[
\angle DCA = \angle BAC = \angle BCA
\]
- Do đó, \(\angle DCA = \frac{1}{2} \angle BCD\).
5. Phân giác trong tam giác cân:
- Trong tam giác cân \(BCD\), đường phân giác \(CA\) sẽ chia góc \(\angle BCD\) thành hai phần bằng nhau:
\[
\angle BCA = \angle DCA = \frac{1}{2} \angle BCD
\]
6. Kết luận:
- Vậy \(CA\) là tia phân giác của góc \(\angle BCD\).
Tóm lại:
Do \(AB = BC\) và các tính chất của tam giác cân và hình thang cân, ta suy ra được \(CA\) là tia phân giác của góc \(\angle BCD\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17097
Đã trả lời bởi chuyên gia
17097 -
 Đã trả lời bởi chuyên gia
16079
Đã trả lời bởi chuyên gia
16079 -
 Đã trả lời bởi chuyên gia
10012
Đã trả lời bởi chuyên gia
10012 -
 Đã trả lời bởi chuyên gia
8884
Đã trả lời bởi chuyên gia
8884 -
 Đã trả lời bởi chuyên gia
8830
Đã trả lời bởi chuyên gia
8830 -
 Đã trả lời bởi chuyên gia
7498
Đã trả lời bởi chuyên gia
7498 -
 Đã trả lời bởi chuyên gia
5904
Đã trả lời bởi chuyên gia
5904


