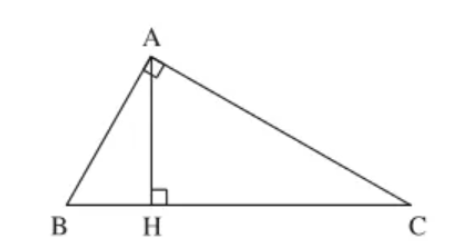
### Giải tam giác ABC

**a) Giải tam giác ABC:**

Ta có tam giác ABC vuông tại A, với AB = 5 cm và AC = 12 cm. Để giải tam giác này, trước tiên ta tìm cạnh BC bằng định lý Pythagore:

\[ BC = \sqrt{AB^2 + AC^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ cm} \]

Vậy cạnh BC = 13 cm.

Để giải tam giác ABC, ta cần tìm các góc B và C:

Sử dụng các hàm lượng giác:
\[ \sin B = \frac{AC}{BC} = \frac{12}{13} \Rightarrow B = \arcsin\left(\frac{12}{13}\right) \]
\[ \cos B = \frac{AB}{BC} = \frac{5}{13} \Rightarrow B = \arccos\left(\frac{5}{13}\right) \]

Tương tự:
\[ \sin C = \frac{AB}{BC} = \frac{5}{13} \Rightarrow C = \arcsin\left(\frac{5}{13}\right) \]
\[ \cos C = \frac{AC}{BC} = \frac{12}{13} \Rightarrow C = \arccos\left(\frac{12}{13}\right) \]

**b) Tính độ dài các đoạn thẳng AH, CH, BH và tính góc HCA:**

Sử dụng công thức độ dài đường cao trong tam giác vuông:
\[ AH = \frac{AB \cdot AC}{BC} = \frac{5 \cdot 12}{13} = \frac{60}{13} \text{ cm} \]

Tính các đoạn CH và BH sử dụng hệ thức lượng trong tam giác vuông:
\[ CH = \sqrt{AC^2 - AH^2} = \sqrt{12^2 - \left(\frac{60}{13}\right)^2} = \sqrt{144 - \frac{3600}{169}} = \sqrt{144 - 21.3} = \sqrt{122.7} \approx 11.08 \text{ cm} \]

\[ BH = \sqrt{AB^2 - AH^2} = \sqrt{5^2 - \left(\frac{60}{13}\right)^2} = \sqrt{25 - \frac{3600}{169}} = \sqrt{25 - 21.3} = \sqrt{3.7} \approx 1.92 \text{ cm} \]

Để tính góc HCA:
\[ \tan(HCA) = \frac{AH}{CH} = \frac{\frac{60}{13}}{11.08} \approx \frac{4.615}{11.08} \approx 0.416 \]

\[ HCA = \arctan(0.416) \approx 22.6^\circ \]

**c) Tính DH, diện tích tam giác BCD:**

- Vẽ đường thẳng \( d \) vuông góc với \( AC \) tại \( C \), \( d \) cắt \( AH \) tại \( D \).
- Kẻ \( BE \) vuông góc với \( CD \) tại \( E \).

Vì \( d \) vuông góc với \( AC \) tại \( C \) và \( AH \) vuông góc với \( BC \), nên \( D \) là giao điểm của hai đường thẳng vuông góc này.

Do đó, \( D \) là trực tâm của tam giác \( ACH \), và ta có:

\[ DH = AH = \frac{60}{13} \text{ cm} \]

- Để tính diện tích tam giác \( BCD \):

Diện tích tam giác \( BCD \) được tính bằng:
\[ S_{BCD} = \frac{1}{2} \times BC \times DH = \frac{1}{2} \times 13 \times \frac{60}{13} = \frac{1}{2} \times 60 = 30 \text{ cm}^2 \]

Vậy, độ dài \( DH = \frac{60}{13} \approx 4.615 \text{ cm} \), và diện tích tam giác \( BCD \) là \( 30 \text{ cm}^2 \).

a) Giải tam giác ABC: Vì tam giác ABC vuông tại A, ta có: (AB^2 + AC^2 = BC^2) (5^2 + 12^2 = BC^2) (25 + 144 = BC^2) (169 = BC^2) (BC = 13)

Vậy ta có tam giác ABC là tam giác vuông tại A, có AB = 5cm, AC = 12cm, BC = 13cm.

b) Tính độ dài các đoạn thẳng AH, CH, BH và tính góc HCA:

Độ dài đoạn thẳng AH: AH là đường cao của tam giác ABC nên AH = ( \frac{AB \times AC}{BC} = \frac{5 \times 12}{13} = \frac{60}{13} ) cm.
Độ dài đoạn thẳng CH: CH = ( AC - AH = 12 - \frac{60}{13} = \frac{36}{13} ) cm.
Độ dài đoạn thẳng BH: BH = ( \sqrt{AB^2 - AH^2} = \sqrt{5^2 - \left(\frac{60}{13}\right)^2} = \sqrt{25 - \frac{3600}{169}} = \sqrt{\frac{169 \times 25 - 3600}{169}} = \sqrt{\frac{4225 - 3600}{169}} = \sqrt{\frac{625}{169}} = \frac{25}{13} ) cm.
Góc HCA: Góc HCA là góc giữa đường cao AH và cạnh AC, ta có: ( \sin(HCA) = \frac{AH}{AC} = \frac{\frac{60}{13}}{12} = \frac{5}{13} ) nên góc HCA là góc nhọn và bằng (\arcsin\left(\frac{5}{13}\right)) rad.
c) Tính DH và diện tích tam giác BCD:

Ta có CD là đường thẳng vuông góc với AC tại C, nên CD = AC = 12cm.
DH là chiều cao của tam giác BCD, ta có DH = ( AH - AC = \frac{60}{13} - 12 = \frac{60 - 156}{13} = \frac{-96}{13} ) cm.
Diện tích tam giác BCD: Diện tích tam giác BCD = ( \frac{1}{2} \times CD \times DH = \frac{1}{2} \times 12 \times \frac{-96}{13} = -\frac{576}{13} ) cm².