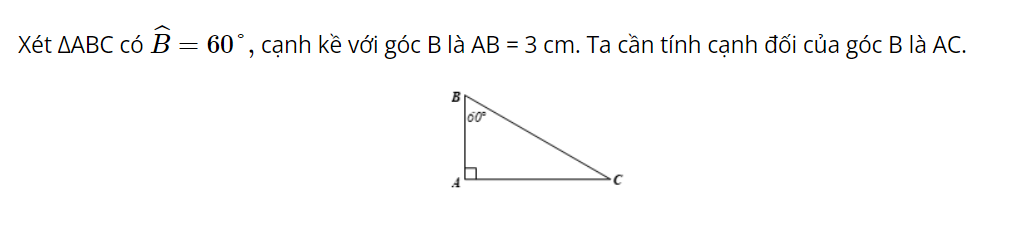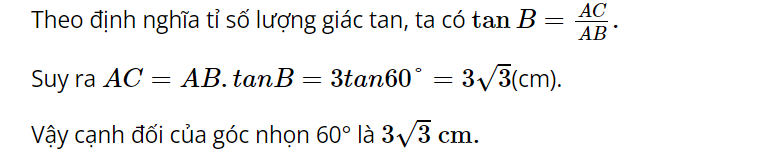1) Tính các tỉ số lượng giác sin, cos, tan, cot của góc nhọn B và C:

a) AB = 8cm; BC = 17cm:

Tìm AC: Sử dụng định lý Pytago: $AC = \sqrt{BC^2 - AB^2} = \sqrt{17^2 - 8^2} = 15cm$

Tỉ số lượng giác góc B:

$sinB = \frac{AC}{BC} = \frac{15}{17}$

$cosB = \frac{AB}{BC} = \frac{8}{17}$

$tanB = \frac{AC}{AB} = \frac{15}{8}$

$cotB = \frac{AB}{AC} = \frac{8}{15}$

Tỉ số lượng giác góc C:

$sinC = \frac{AB}{BC} = \frac{8}{17}$

$cosC = \frac{AC}{BC} = \frac{15}{17}$

$tanC = \frac{AB}{AC} = \frac{8}{15}$

$cotC = \frac{AC}{AB} = \frac{15}{8}$

b) AC = 0.9m; AB = 1.2cm:

Tìm BC: Sử dụng định lý Pytago: $BC = \sqrt{AB^2 + AC^2} = \sqrt{1.2^2 + 0.9^2} = 1.5cm$

Tỉ số lượng giác góc B:

$sinB = \frac{AC}{BC} = \frac{0.9}{1.5} = 0.6$

$cosB = \frac{AB}{BC} = \frac{1.2}{1.5} = 0.8$

$tanB = \frac{AC}{AB} = \frac{0.9}{1.2} = 0.75$

$cotB = \frac{AB}{AC} = \frac{1.2}{0.9} = \frac{4}{3}$

Tỉ số lượng giác góc C:

$sinC = \frac{AB}{BC} = \frac{1.2}{1.5} = 0.8$

$cosC = \frac{AC}{BC} = \frac{0.9}{1.5} = 0.6$

$tanC = \frac{AB}{AC} = \frac{1.2}{0.9} = \frac{4}{3}$

$cotC = \frac{AC}{AB} = \frac{0.9}{1.2} = 0.75$

2) Tính cạnh đối diện góc 60 độ:

Sử dụng tỉ số lượng giác: $tan60^\circ = \frac{cạnh đối}{cạnh kề} = \sqrt{3}$

Thay giá trị: $\sqrt{3} = \frac{cạnh đối}{3}$

Tính cạnh đối: $cạnh đối = 3\sqrt{3} cm$

3) Tính độ dài cạnh huyền:

Sử dụng tỉ số lượng giác: $sin30^\circ = \frac{cạnh đối}{cạnh huyền} = \frac{1}{2}$

Thay giá trị: $\frac{1}{2} = \frac{5}{cạnh huyền}$

Tính cạnh huyền: $cạnh huyền = 5 \times 2 = 10cm$

4) Tính góc giữa đường chéo và cạnh ngắn hơn của HCN:

Vẽ hình: Hình chữ nhật có chiều dài 3, chiều rộng $\sqrt{3}$. Đường chéo chia hình chữ nhật thành hai tam giác vuông.

Tỉ số lượng giác: $tan \alpha = \frac{cạnh đối}{cạnh kề} = \frac{\sqrt{3}}{3}$ (với $\alpha$ là góc cần tìm)

Tìm góc: $\alpha = arctan(\frac{\sqrt{3}}{3}) = 30^\circ$

5) Tính các góc của hình thoi:

Vẽ hình: Hình thoi có hai đường chéo dài $2\sqrt{3}$ và 2.

Tính góc:

Góc giữa hai đường chéo của hình thoi là $90^\circ$.

Hình thoi được chia thành 4 tam giác vuông bằng nhau.

Xét một tam giác vuông, ta có: $tan \alpha = \frac{cạnh đối}{cạnh kề} = \frac{1}{\sqrt{3}}$ (với $\alpha$ là góc cần tìm)

Tìm góc: $\alpha = arctan(\frac{1}{\sqrt{3}}) = 30^\circ$

Góc của hình thoi là $2\alpha = 2 \times 30^\circ = 60^\circ$