Quảng cáo
2 câu trả lời 160
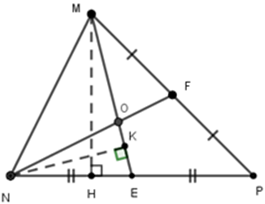
Cho biết: \( MH \) là đường cao từ \( M \) đến cạnh \( BC \), \( NK \) là đường cao từ \( N \) đến cạnh \( ME \).
Hai đoạn thẳng trung điểm \( ME \) và \( NF \) giao nhau tại \( O \), vậy \( O \) là trọng tâm của tam giác \( MNP \), do đó \( \frac{MO}{MC} = \frac{2}{3} \).
Vì \( ME \) là đoạn trung điểm tương ứng với cạnh \( NP \), \( E \) là trung điểm của \( NP \), do đó \( NP = 2NE \).
Chúng ta có:
\[
\frac{SMN}{OM} = \frac{1}{2} \cdot \frac{NK}{MO} \quad \text{và} \quad \frac{SMN}{ME} = \frac{1}{2} \cdot \frac{NK}{ME}
\]
\[
\frac{SMN}{NK} = \frac{1}{2} \cdot \frac{NK}{ME} \quad \text{và} \quad \frac{SMN}{NK} = \frac{2}{3} \cdot \frac{NK}{ME}
\]
\[
\frac{SMN}{NK} = \frac{1}{2} \cdot \frac{2}{3} = \frac{1}{3} \quad \Rightarrow \quad \frac{SMN}{ME} = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6}
\]
Từ đây, chúng ta có thể kết luận:
\[
S_{MNP} = 2 \cdot S_{MNE} = 3 \cdot S_{MNO} \quad \Rightarrow \quad S_{MNP} = 3 \cdot 8 = 24 \, \text{cm}^2
\]
Gọi $S_{MNO}$ là diện tích của tam giác $MNO$, và $S_{MNP}$ là diện tích của tam giác $MNP$.
Vì đường trung tuyến $ME$ chia tam giác $MNP$ thành hai tam giác $MNE$ và $MPE$ ta có:
$S_{MNP} = 4 \cdot S_{MNE}$
Tương tự, đường trung tuyến $NF$ chia tam giác $MNP$ thành hai tam giác $MNF$ và $NPF$, nên:
$S_{MNP} = 4 \cdot S_{MNF}$
Vì tam giác $MNO$ là đều và có diện tích $S_{MNO} = 8 \, \text{cm}^2$, ta có:
$S_{MNE} = S_{MNF} = \frac{1}{2} \cdot S_{MNO} = 4 \, \text{cm}^2$
Do đó:
$S_{MNP} = 4 \cdot S_{MNE} = 4 \cdot 4 = 16 \, \text{cm}^2$
Vậy diện tích của tam giác $MNP$ là 16 cm².
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


