Cho tứ diện ABCD. Gọi E, F, G lần lượt là các điểm thuộc ba cạnh AB, AC, BD sao cho EF cắt BC tại I, AD cắt EG tại H. Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Quảng cáo
1 câu trả lời 69
1 năm trước
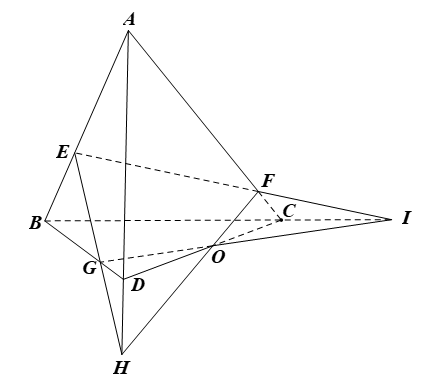
Gọi O là giao điểm của HF và IG.
Ta có:
⦁ O ∈ HF, mà HF ⊂ (ACD), suy ra O ∈ (ACD);
⦁ O ∈ IG, mà IG ⊂ (BCD), suy ra O ∈ (BCD).
Do đó, O ∈ (ACD) ∩ (BCD) (1)
Mặt khác, (ACD) ∩ (BCD) = CD (2)
Từ (1) và (2), suy ra O ∈ CD.
Lại có O = HF ∩ IG nên O là giao điểm của ba đường thẳng CD, IG, HF.
Vậy ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134838
Đã trả lời bởi chuyên gia
134838 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
75920
Đã trả lời bởi chuyên gia
75920 -
 Đã trả lời bởi chuyên gia
71641
Đã trả lời bởi chuyên gia
71641 -
 Đã trả lời bởi chuyên gia
47575
Đã trả lời bởi chuyên gia
47575
Gửi báo cáo thành công!


