Lời giải

a) Lấy đối xứng đồ thị hàm số y = cos x qua trục hoành ta được đồ thị hàm số y = – cos x.

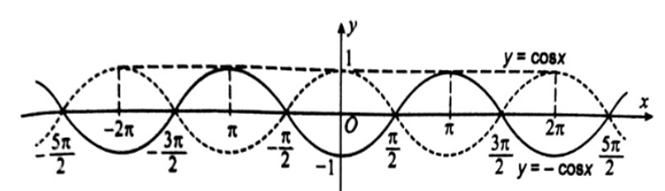
Trong hình trên, đồ thị hàm số y = cos x là đường nét đứt còn đồ thị hàm số y = – cos x là đường nét liền.

b) Ta có \(y = \left| {\cos x} \right| = \left\{ \begin{array}{l}\cos x\,\,\,\,\,\,\,\,khi\,\,\,\cos x \ge 0\\ - \cos x\,\,\,\,khi\,\,\,\cos x < 0\end{array} \right.\).

Từ đó, để vẽ đồ thị hàm số y = |cos x| đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó giữ nguyên phần đồ thị hàm số y = cos x ở phía trên trục Ox và lấy đối xứng qua trục Ox phần đồ thị hàm số y = cos x ở phía dưới trục Ox.

Trong hình dưới đây, đồ thị hàm số y = |cos x| là đường nét liền.

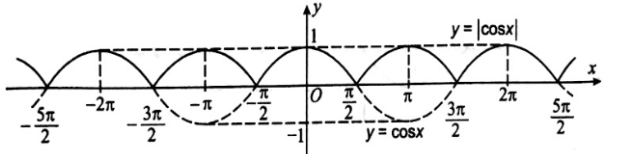
c) Để vẽ đồ thị hàm số y = cos x + 1, đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó dịch chuyển đồ thị này dọc theo trục Oy lên phía trên 1 đơn vị, ta được đồ thị hàm số y = cosx + 1. Trong hình dưới đây, đồ thị hàm số y = cos x + 1 là đường nét liền.

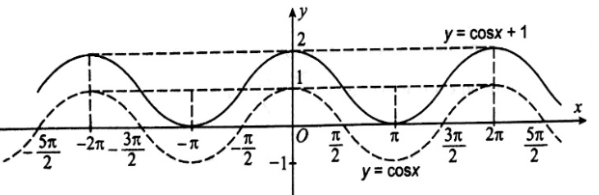
d) Để vẽ đồ thị hàm số \(y = \cos \left( {x + \frac{\pi }{2}} \right)\) đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó dịch chuyển đồ thị này dọc theo trục Ox sang bên trái \(\frac{\pi }{2}\) đơn vị ta sẽ được đồ thị hàm số \(y = \cos \left( {x + \frac{\pi }{2}} \right)\). Trong hình vẽ dưới đây đồ thị hàm số \(y = \cos \left( {x + \frac{\pi }{2}} \right)\) là đường nét liền.

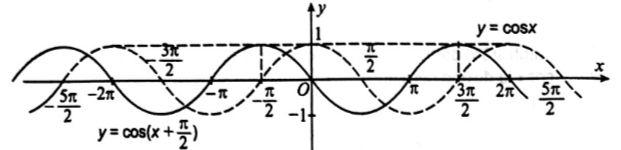
Chú ý rằng \(\cos \left( {x + \frac{\pi }{2}} \right) = - \sin x\) nên đồ thị hàm số \(y = \cos \left( {x + \frac{\pi }{2}} \right)\) cũng có thể có được bằng cách lấy đối xứng đồ thị hàm số y = sin x qua trục Ox.