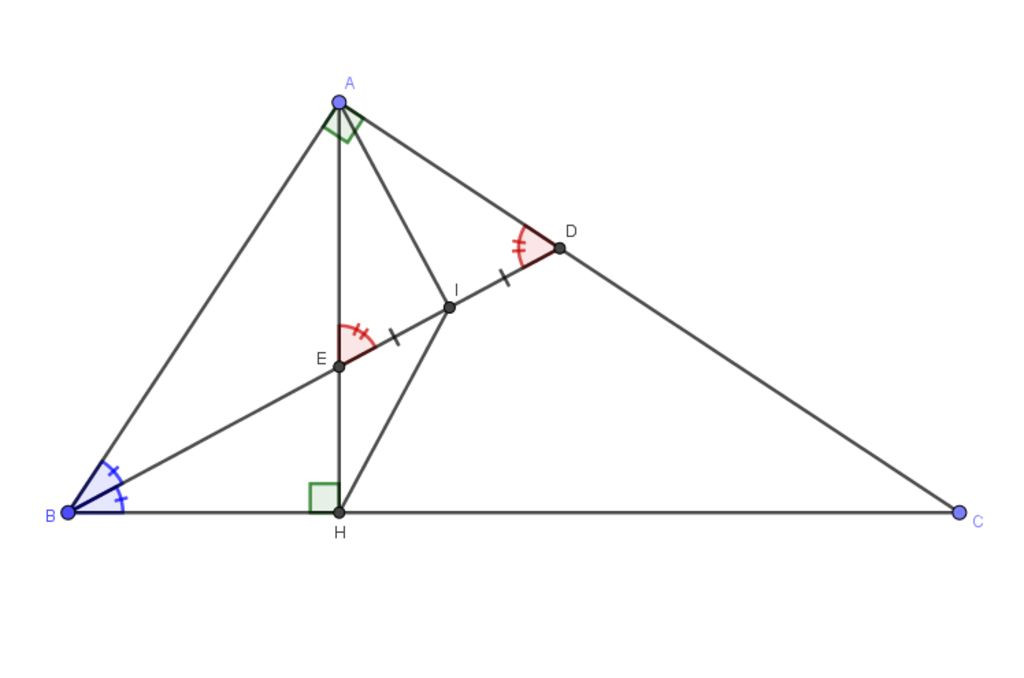
Bài 10. Cho ∆ABC vuông tại A. Kẻ đường cao AH. Đường phân giác của ABC cắt AC tại D và cắt AH tại E.
a) Biết AB = 9cm, BC = 15cm. Tính AC?
b) Chứng minh: ΔΑΒC ΔΗΒΑ
c) Gọi I là trung điểm của ED. C/m EI/EA = EH/EB
d). Chứng minh: BIH = ACBBài 10. Cho ∆ABC vuông tại A. Kẻ đường cao AH. Đường phân giác của ABC cắt AC tại D và cắt AH tại E.
a) Biết AB = 9cm, BC = 15cm. Tính AC?
b) Chứng minh: ΔΑΒC ΔΗΒΑ
c) Gọi I là trung điểm của ED. C/m EI/EA = EH/EB
d). Chứng minh: BIH = ACB
Quảng cáo
1 câu trả lời 2972
a)
Ta có:
AD là đường phân giác của ∆ABC
nên BD = CD.
Vì ∆ABC vuông tại A nên theo định lý Pythagore, ta có:
AB² + AC² = BC²
9² + AC² = 15²
81 + AC² = 225
AC² = 144
AC = 12 cm
b)
Ta có:
∠BAC = ∠BAH (cùng nằm trên cùng cạnh AB)
∠ABC = ∠BHA (cùng nằm trên cùng cạnh BH)
AB = AB (cạnh chung)
Vậy theo điều kiện A, ta có ΔABC ≅ ΔHBA
d)
Xét ΔABD vuông tại A có:

⇒ΔAED cân tại A
Ta lại có: I là trung điểm cạnh đáy DE
⇒AI⊥DE
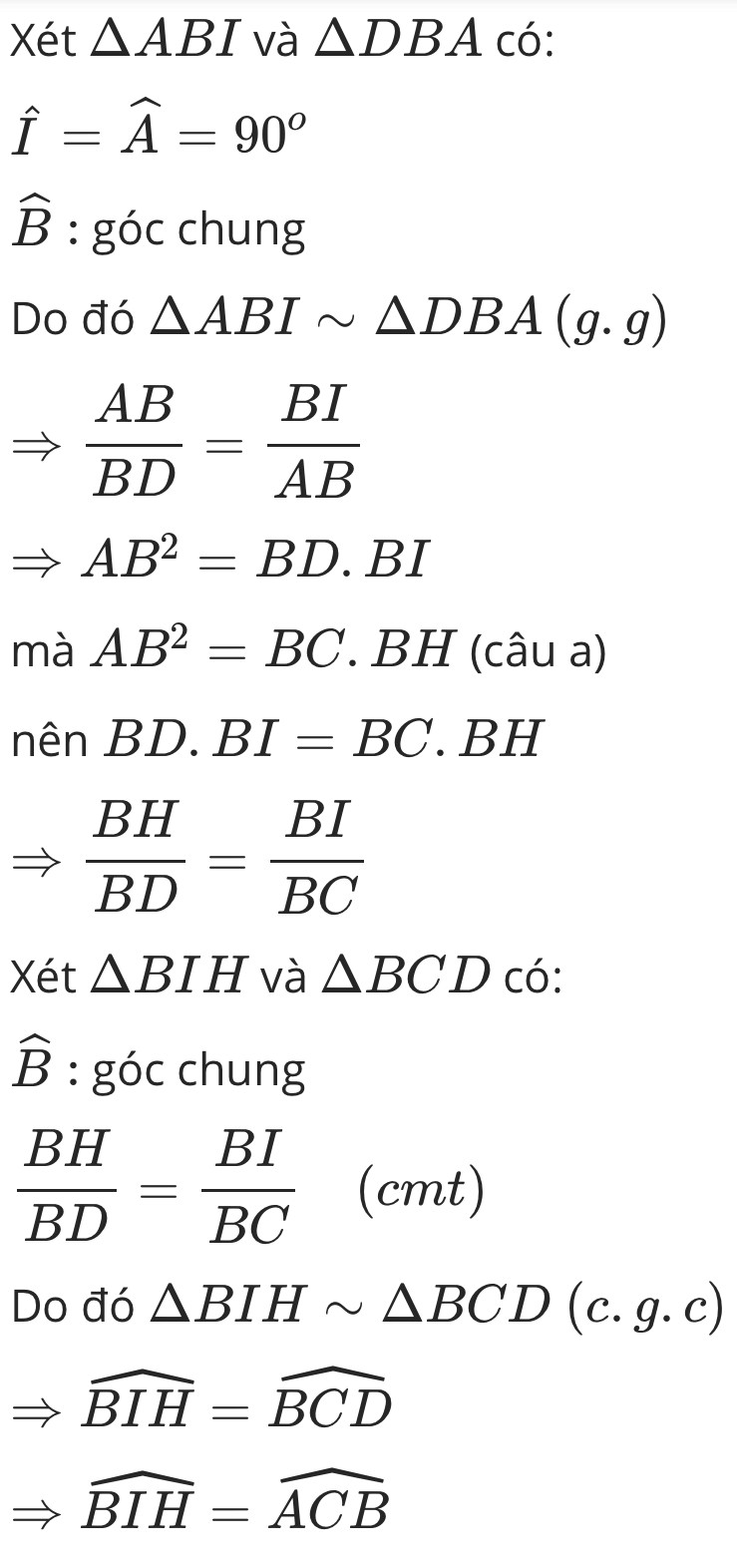
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17097
Đã trả lời bởi chuyên gia
17097 -
 Đã trả lời bởi chuyên gia
16079
Đã trả lời bởi chuyên gia
16079 -
 Đã trả lời bởi chuyên gia
10012
Đã trả lời bởi chuyên gia
10012 -
 Đã trả lời bởi chuyên gia
8884
Đã trả lời bởi chuyên gia
8884 -
 Đã trả lời bởi chuyên gia
8830
Đã trả lời bởi chuyên gia
8830 -
 Đã trả lời bởi chuyên gia
7498
Đã trả lời bởi chuyên gia
7498 -
 Đã trả lời bởi chuyên gia
5904
Đã trả lời bởi chuyên gia
5904


