cho tam giác abc vuông tại a và góc b bằng 60 độ . phân giác góc b cắt ac tại d kẻ đường vuông góc de đến bc e thuộc bc a) chứng minh ba=be , da=de b) chứng minh tam giác bdc là tam giác cân vì sao ? c) so sánh độ dài de và bc
Quảng cáo
2 câu trả lời 1323
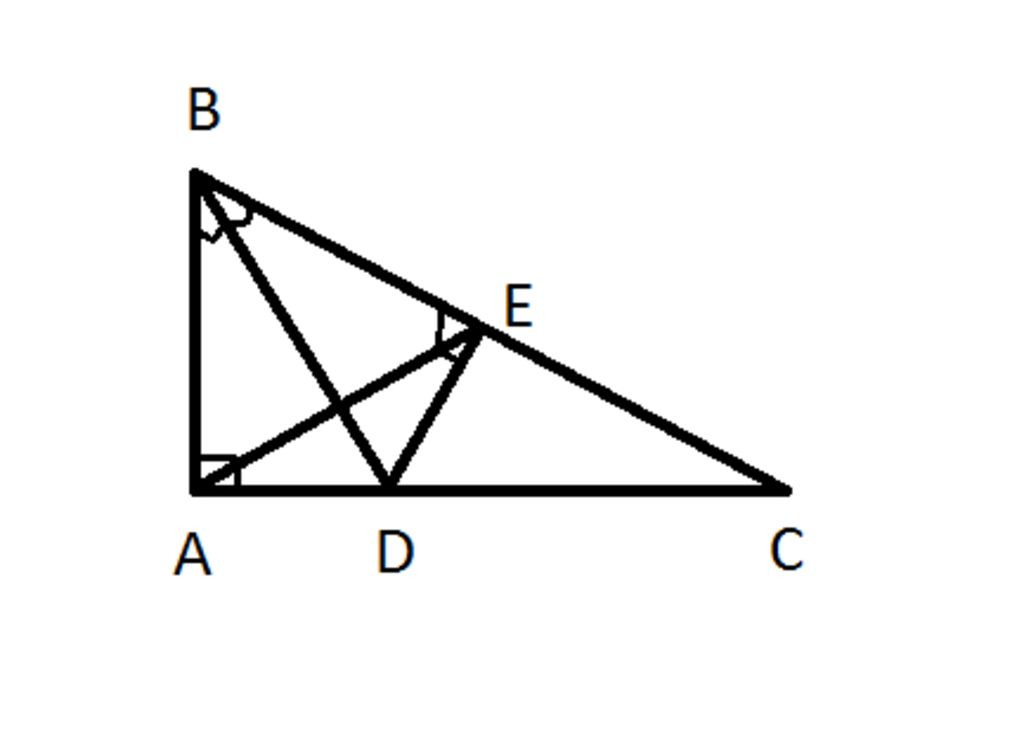
a,
Xét ΔABD và ΔEBD có:
=> ΔABD = ΔEBD (ch-gn) (1)
=> BA = BE
và DA = DE
b)
Ta có:
=> DE là phân giác của tam giác DBC
Mà DE cũng là đường cao hạ từ D
=> DBC cân tại D
c,
Ta có:
DE là đường trung tuyến của tam giác DBC
=> BC = 2.BE
=> BC > BE
Xét tam giác BDE có:
=> DE < BE
=> DE < BC
a) Chứng minh ba=be, da=de:
Ta có tam giác ABC vuông tại A và góc B bằng 60 độ.
Phân giác góc B cắt AC tại D. Kẻ đường vuông góc DE đến BC tại E.
Vì AD là phân giác của góc BAC, ta có:
∠BAD = ∠CAD
Vì tam giác ABC vuông tại A, ta có:
∠BAC = 90 độ
Vì góc B bằng 60 độ, ta có:
∠BAD = ∠CAD = 30 độ
Do đó, tam giác ABD và tam giác ACD là tam giác cân tại A.
Vì vậy, ta có:
AB = AD AC = AD
Trong tam giác ADE vuông tại D, ta có:
∠DAE = 90 độ
Vì tam giác ABD và tam giác ACD là tam giác cân, nên ta có:
AB = AD = AE
AC = AD = AE
Vậy, ta chứng minh được ba=be, da=de.
b) Chứng minh tam giác BDC là tam giác cân:
Trong tam giác BDC, ta có:
BD = CD (vì tam giác ABD và tam giác ACD là tam giác cân)
Và ∠DBC = ∠DCB = 30 độ (vì góc B bằng 60 độ và BD là phân giác của góc B)
Vậy, tam giác BDC là tam giác cân.
c) So sánh độ dài DE và BC:
Vì tam giác BDC là tam giác cân, nên ta có BD = CD.
Do đó, DE là đường cao của tam giác BDC, nên DE sẽ bằng một nửa độ dài BC.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835
Gửi báo cáo thành công!


