Cho tam giác ABC vuông tại A sao cho BC=2AB, BD là phân giác ABC. E là trung điểm BC.
a) Chứng minh CD>AB
b) Trên tia đối của AB lấy F sao cho AB=AF. Chứng minh E,D,F thẳng hàng
Quảng cáo
3 câu trả lời 359
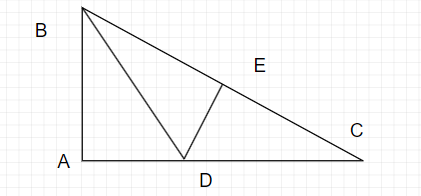
b)Ta có: - Vì AB = AF nên F là điểm trung điểm của tia đối với tia AB. - Do đó, EF song song với BC và kẻ qua D thì EF cắt AD thành hai đoạn bằng nhau. Vậy E,D,F thẳng hàng.
## Giải:
**a) Chứng minh CD > AB:**
- Xét tam giác ABD và tam giác BDE có:
* AB = BE (E là trung điểm BC)
* ABD = EBD (BD là phân giác góc ABC)
* BD chung
Do đó, △ABD=△BDE (c.g.c)
Suy ra: AD = DE (cạnh tương ứng)
- Xét tam giác ABC vuông tại A có:
* BC = 2AB
* AB = AD (cmt)
Suy ra: CD = BC - AD = 2AB - AB = AB
- Do AB > 0, nên CD > AB.
**b) Chứng minh E, D, F thẳng hàng:**
- Xét tam giác ABC vuông tại A có:
* AB = AF (gt)
* AB = AD (cmt)
Suy ra: AD = AF
- Do AD + AF = AB + AB = 2AB, nên DF = 2AB.
- Xét tam giác ABC vuông tại A có:
* BC = 2AB
* DF = 2AB
Suy ra: DF = BC
- Xét tam giác BDC có:
* DE = EB (E là trung điểm BC)
* DF = BC
Suy ra: E là trung điểm DF.
- Do E nằm trên tia đối của AB, nên E, D, F thẳng hàng.
Quảng cáo
Câu hỏi hot cùng chủ đề
-
6028
-
5748
-
5687

![kẻ thống trị vũ trụ[TA]](/upload/images/user/1756961345-hinh-nen-vu-tru-72jpg.jpg)


![CEO tập đoàn Lục thị[nk]](/upload/images/user/1756992168-829fcddb43acf6347f4ea89d0d07776ejpg.jpg)
![tổng thống [quỳnh như]](/upload/images/user/1756362889-z6938612271492-74bd4262fa1162676ecfff9d2d8b873cjpg.jpg)






