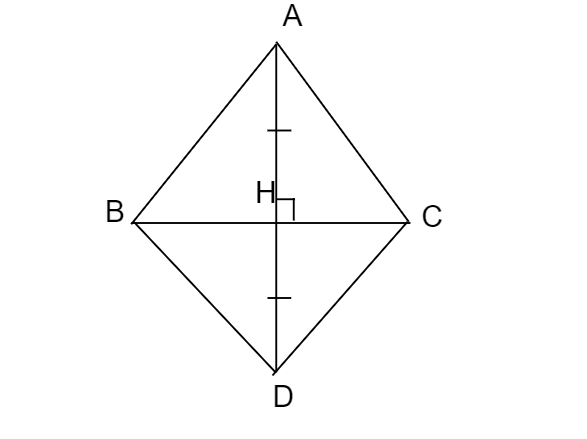
B7: Cho tam giác ABC có ba góc đều nhọn, AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA=HD
a) C/M: BC và CB lần lượt là các tia phân giác của các góc ABD và ACD.
b) C/M: CA = CD và BD = BA
c) Cho góc ACB=45 độ. Tính góc ADC.
d) Đường vuông góc AH phải có thêm điều kiện gì thì AB//CD?
Quảng cáo
2 câu trả lời 6479
a/ Xét tam giác ABH và tam giác DBH có:
BH: chung
ˆAHBAHB^=ˆDHBDHB^=90độ
AH = HD (GT)
Vậy tam giác ABH = tam giác DBH (c.g.c)
=> ˆABHABH^=ˆDBHDBH^ => BC là phân giác góc ABD
Xét tam giác ACH và tam giác DCH có:
CH: cạnh chung
ˆAHCAHC^=ˆDHCDHC^=90độ
AH = HD (GT)
Vậy tam giác ACH = tam giác DCH (c.g.c)
=> ˆACHACH^=ˆDCHDCH^=> CB là phân giác góc ACD
b/ Ta có: tam giác ABH = tam giác DBH (đã chứng minh trên)
=> BA = BD (2 cạnh tương ứng)
Ta có: tam giác ACH = tam giác DCH (đã chứng minh trên)
=> CA = CD (2 cạnh tương ứng)
c/ Ta có: tam giác ACH = tam giác DCH
=> ˆACHACH^=ˆDCHDCH^=45độ
Trong tam giác CHD có:
ˆCC^+ˆHH^+ˆDD^=180độ
45độ + 90độ + góc D = 180độ
=> góc ADC = 45độ
d/ Đường cao AH phải có thêm điều kiện BH = HC => chứng minh tam giác ABH = CDH để AB//CD
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8640
Đã trả lời bởi chuyên gia
8640 -
 Đã trả lời bởi chuyên gia
7637
Đã trả lời bởi chuyên gia
7637 -
6856
-
 Đã trả lời bởi chuyên gia
6553
Đã trả lời bởi chuyên gia
6553 -
 Đã trả lời bởi chuyên gia
6331
Đã trả lời bởi chuyên gia
6331