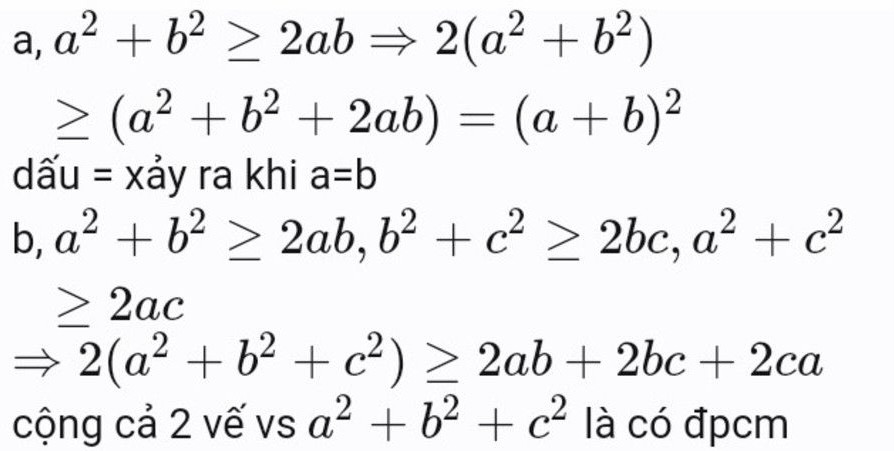Câu 10. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Quảng cáo
2 câu trả lời 200
Chứng minh bất đẳng thức:
a) (a + b)² ≤ 2(a² + b²)
Cách 1:
Biến đổi vế trái:
(a + b)² = a² + 2ab + b²
So sánh với vế phải:
a² + 2ab + b² ≤ 2a² + 2b²
a² - 2ab + b² ≤ 0
Biến đổi vế trái thành vế phải:
(a - b)² ≥ 0
Luôn đúng với mọi a, b.
Cách 2:
Sử dụng bất đẳng thức Cauchy-Schwarz:
Với hai số dương a và b, ta có:
(1 + 1)(a² + b²) ≥ (a + b)²
=> (a + b)² ≤ 2(a² + b²)
b) (a + b + c)² ≤ 3(a² + b² + c²)
Cách 1:
Biến đổi vế trái:
(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc
So sánh với vế phải:
a² + b² + c² + 2ab + 2ac + 2bc ≤ 3a² + 3b² + 3c²
a² - 2ab + b² + a² - 2ac + c² + b² - 2bc + c² ≤ 0
Biến đổi vế trái thành vế phải:
(a - b)² + (a - c)² + (b - c)² ≥ 0
Luôn đúng với mọi a, b, c.
Cách 2:
Sử dụng bất đẳng thức Cauchy-Schwarz:
Với ba số dương a, b, c, ta có:
(1 + 1 + 1)(a² + b² + c²) ≥ (a + b + c)²
=> (a + b + c)² ≤ 3(a² + b² + c²)
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
7856
-
6019