Question

Đã trả lời bởi chuyên gia

Answer 1

Trước hết ta chứng minh một kết quả trong hình học phẳng: Trong hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh.

Xét hình bình hành MNPQ:

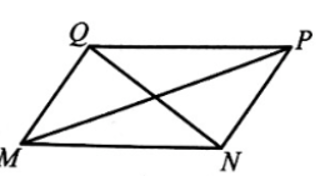
Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh. (ảnh 1)

Áp dụng định lí côsin trong các tam giác MPQ và QPN, ta có:

MP2 = QM2 + QP2 – 2QM . QP . cos $\hat{M Q P}$

QN2 = PQ2 + PN2 – 2PQ . PN . cos $\hat{Q P N}$

Do QM = PN và $\cos \hat{M Q P} = - \cos \hat{Q P N}$ (do hai góc bù nhau) nên ta có:

MP2 + QN2 = 2(QM2 + QP2).

Xét hình hộp ABCD.A'B'C'D':

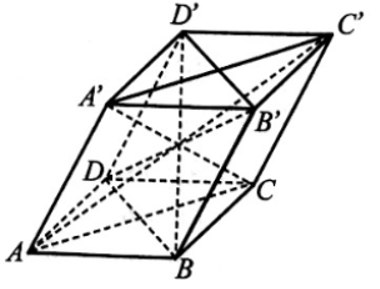
Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh. (ảnh 2)

Áp dụng kết quả trên cho hai hình bình hành AA'C'C và BB'D'D ta được:

AC'2 + A'C2 = 2(AA'2 + A'C'2)

BD'2 + B'D2 = 2(BB'2 + B'D'2)

Suy ra AC'2 + A'C2 + BD'2 + B'D2 = 4AA'2 + 2(A'C'2 + B'D'2) (do AA' = BB').

Mặt khác, trong hình bình hành A'B'C'D', ta có: A'C'2 + B'D'2 = 2(A'B'2 + A'D'2).

Vậy AC'2 + A'C2 + BD'2 + B'D2 = 4AA'2 + 4A'B'2 + 4A'D'2.

Từ đó suy ra điều phải chứng minh.

...Xem thêm

Answer 2