Cho ba mặt phẳng (P), (Q) và (R) đôi một song song. Hai đường thẳng phân biệt d và d' cắt ba mặt phẳng lần lượt tại A, B, C và A', B', C' (C khác C'). Gọi D là giao điểm của AC' và (Q) (H.4.48).
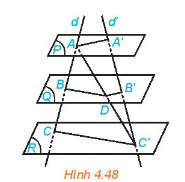
a) Các cặp đường thẳng BD và CC', B'D và AA' có song song với nhau không?
b) Các tỉ số \(\frac{{AB}}{{BC}},\,\,\frac{{AD}}{{DC'}}\) và \(\frac{{A'B'}}{{B'C'}}\) có bằng nhau không?
Quảng cáo
3 câu trả lời 192
Hai đường thẳng d, d' cắt ba mặt phẳng (P), (Q), (R) đôi một song song lần lượt tại A, B, C và A', B', C'. Do đó, áp dụng định lí Thales, ta có: ABA'B'=BCB'C'=ACA'C'���'�'=���'�'=���'�'.
Suy ra B'C'=A'B'.BCAB=3.62=9�'�'=�'�'.����=3.62=9.
Vậy B'C' = 9 cm.
a) Mặt phẳng (ACC') lần lượt cắt hai mặt phẳng song song (Q) và (R) theo hai giao tuyến BD và CC'. Do đó, BD // CC'.
Mặt phẳng AC'A' lần lượt cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến AA' và B'D. Do đó, B'D // AA'.
b) Xét tam giác ACC' có BD // CC', theo định lý Thalés trong tam giác ta suy ra ABBC=ADDC′����=����′
Tương tự, xét tam giác AA'C' có B'D // AA', ta suy ra ADDC′=A′B′B′C′����′=�′�′�′�′.
Vậy ABBC=ADDC′=A′B′B′C′����=����′=�′�′�′�′.
Lời giải:
a) Mặt phẳng (ACC') lần lượt cắt hai mặt phẳng song song (Q) và (R) theo hai giao tuyến BD và CC'. Do đó, BD // CC'.
Mặt phẳng AC'A' lần lượt cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến AA' và B'D. Do đó, B'D // AA'.
b) Xét tam giác ACC' có BD // CC', theo định lý Thalés trong tam giác ta suy ra \(\frac{{AB}}{{BC}} = \frac{{AD}}{{DC'}}\)
Tương tự, xét tam giác AA'C' có B'D // AA', ta suy ra \(\frac{{AD}}{{DC'}} = \frac{{A'B'}}{{B'C'}}\).
Vậy \(\frac{{AB}}{{BC}} = \frac{{AD}}{{DC'}} = \frac{{A'B'}}{{B'C'}}\).Quảng cáo
Bạn muốn hỏi bài tập?


