Quảng cáo
1 câu trả lời 1185
2 năm trước
Thực hiện phép chia đa thức như sau:
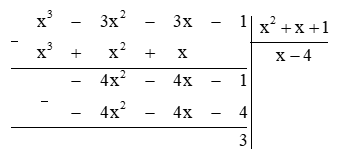
Để đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1 thì 3 ⋮ (x2 + x + 1).
Tức là x2 + x + 1 ∈ Ư(3) = {–3; 3; –1; 1}.
Do x > 0 nên x2 + x + 1 > 1
Do đó x2 + x + 1 = 3
x2 + x – 2 = 0
x2 – x + 2x – 2 = 0
x(x – 1) + 2(x – 1) = 0
(x – 1)(x + 2) = 0
Suy ra x = 1 (thỏa mãn) hoặc x = – 2 (loại).
Vậy x = 1 thì đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669
Gửi báo cáo thành công!


