Cho tam giác ABC có AB=AC.Vẽ tia phân giác của góc A cắt BC ở D. Gọi góc M là một điểm nằm giữa A và D
a, chứng minh tam giác ABM=AMC
b,chứng minh MBD=MCD
Quảng cáo
2 câu trả lời 2313
`a,`
Xét `\triangle` `AMB` và `\triangle` `AMC` có:
`AB= AC` $(gt)$
`hat(BAM) = hat(MAC)` `(AD` là phân giác của `hat(A)` `)`
`AM - ` chung
`=>` `\triangle` `AMB` `=` `\triangle` `AMC` `(c.g.c)`
`b,`
Do: `\triangle` `AMB` `=` `\triangle` `AMC` `(cmt)`
`=>` `MB = MC` `(2` cạnh tương ứng `)`
Xét `\triangle` `MBD` và `\triangle` `MCD` có:
`MB = MC` `(cmt)`
`hat(BMD) = hat(DMC)` `(cmt)`
`MD - ` chung
`=>` `\triangle` `MBD` `=` `\triangle` `MCD` `(c.g.c)`
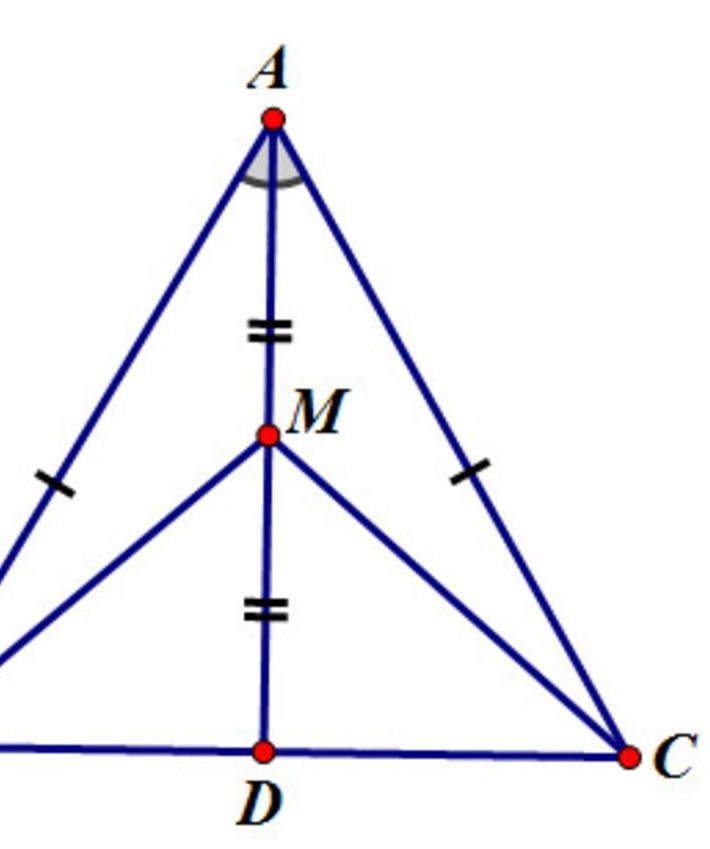
a, xét ABM và AMC ta có:
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
12233
-
5721
-
4825


