a) chứng minh OI _l_ AB
b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OI
Chứng minh BC _l_ Ox
Quảng cáo
2 câu trả lời 1688
a) Xét `ΔOAI` và `ΔOBI`có:
`\hat(AOI) = \hat(BOI)`( OI là tia phân giác của `xOy`)
`OA = OB` (gt)
`OI` chung
`=> ΔOAI = ΔOBI (c -g-c)`
`=>\hat(OIA)=\hat(OIB)` ( 2 góc tương ứng)
Mà `\hat(OIA)+\hat(OIB)=180^o`(kề bù) nên
`=>\hat(OIA)=\hat(OIB)=(180^o)/2=90^o`
`=> OI⊥AB`
b) Xét `ΔOBA` có:
`AD` là đường cao tương ứng với `OB` (gt)
`OI` là đường cao tương ứng với `AB` (cmt)
`C` là giao điểm của `AD, OI` (gt)
`=> C` là trực tâm của giao điểm của `ΔOBA`
`=>BC⊥Ox`
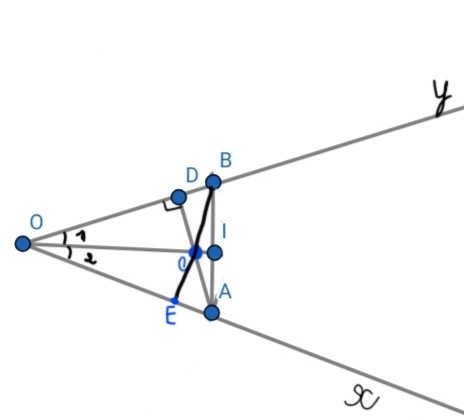
a. Xét ∆OAI và ∆OBI, ta có:
OI: cạnh chung
^O1 = ^O2 ( OI là phân giác ^xOy )
OA = OB ( gt )
=> ∆OAI = ∆OBI ( c.g.c )
=> ^OIA = ^OIB ( 2 góc tương ứng )
Mà: ^OIA + ^OIB = 180⁰ ( kề bù ).
=> ^OIA = ^OIB = = 90⁰
=> OI ( đpcm ).
b.
Xét∆ OAB, ta có:
OI, AD là đường cao
Mà: OI và AD cắt nhau tại C
=> C là trực tâm của ∆OAB
=> BC Ox ( đpcm )
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


