a) Chứng minh: Tam giác DEM = Tam giác DHM
b) Gọi K là giao điểm của tia DE và tia MH. Tam giác KMF là tam giác gì? Vì sao?
c) Cm: KM+ ME < KF
Quảng cáo
2 câu trả lời 442
Mình gửi bạn
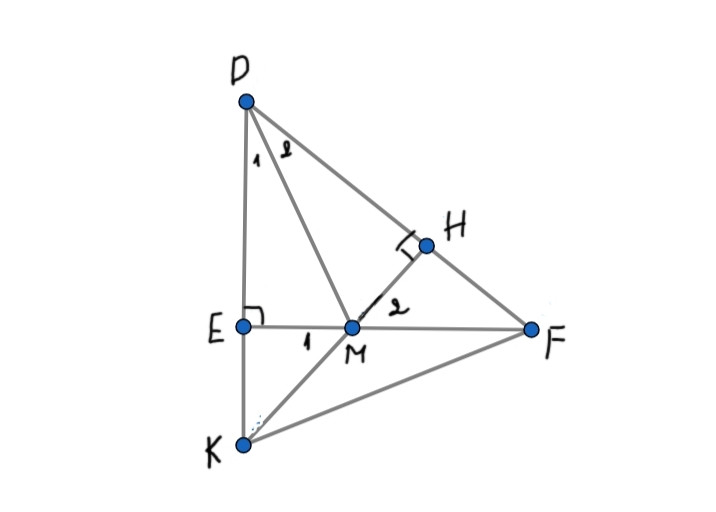
a.
Xét ∆DEM vuông tại E và ∆DHM vuông tại H, ta có:
DM: cạnh chung
= ( DM là phân giác ^D )
=> ∆DEM = ∆DHM ( cạnh huyền - góc nhọn )
b.
Xét ∆EMK vuông tại E và ∆HMF vuông tại H, ta có:
EM = HM ( ∆DEM = ∆DHM )
^M1 = ^M2 ( đối đỉnh )
=> ∆EMK = ∆HMF ( cạnh góc vuông - góc nhọn kề )
=> MK = MF ( 2 cạnh tương ứng )
=> ∆KMF cân tại M
c.
Xét ∆EKF vuông tại E, ta có:
EF < KF ( quan hệ đường xiên và đường vuông góc)
=> EM + MF < KF
Mà: MF = MK ( ∆EMK = ∆HMF )
=> KM + ME < KF ( đpcm )
a, Xét 2 tam giác vuông DEM và HEM có:
ME cạnh chung
ˆDEM=ˆHEM(gt)
=> tam giác DEM=tam giác HEM(CH-GN)
b, vì tam giác DEM=tam giác HEM(câu a) suy ra MD=MH(2 cạnh tương ứng)
c, trong tam giác FKE có: FD,KH là 2 đường cao cắt nhau tại M
=> K,M,H thẳng hàng
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


