cho tam giác ABC cân tại A . Trên tia đối caut tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cah BD=CE. Kẻ BH ( T nằm ngược tại ko có dấu ấy) AD tại H, CK ( chữ T nằm ngược) AE tại K. Chứng minh
A tam giác BHD= tam giác CKE
B tam giác ABH= tam giác AKC
C BC || HK
Quảng cáo
1 câu trả lời 340
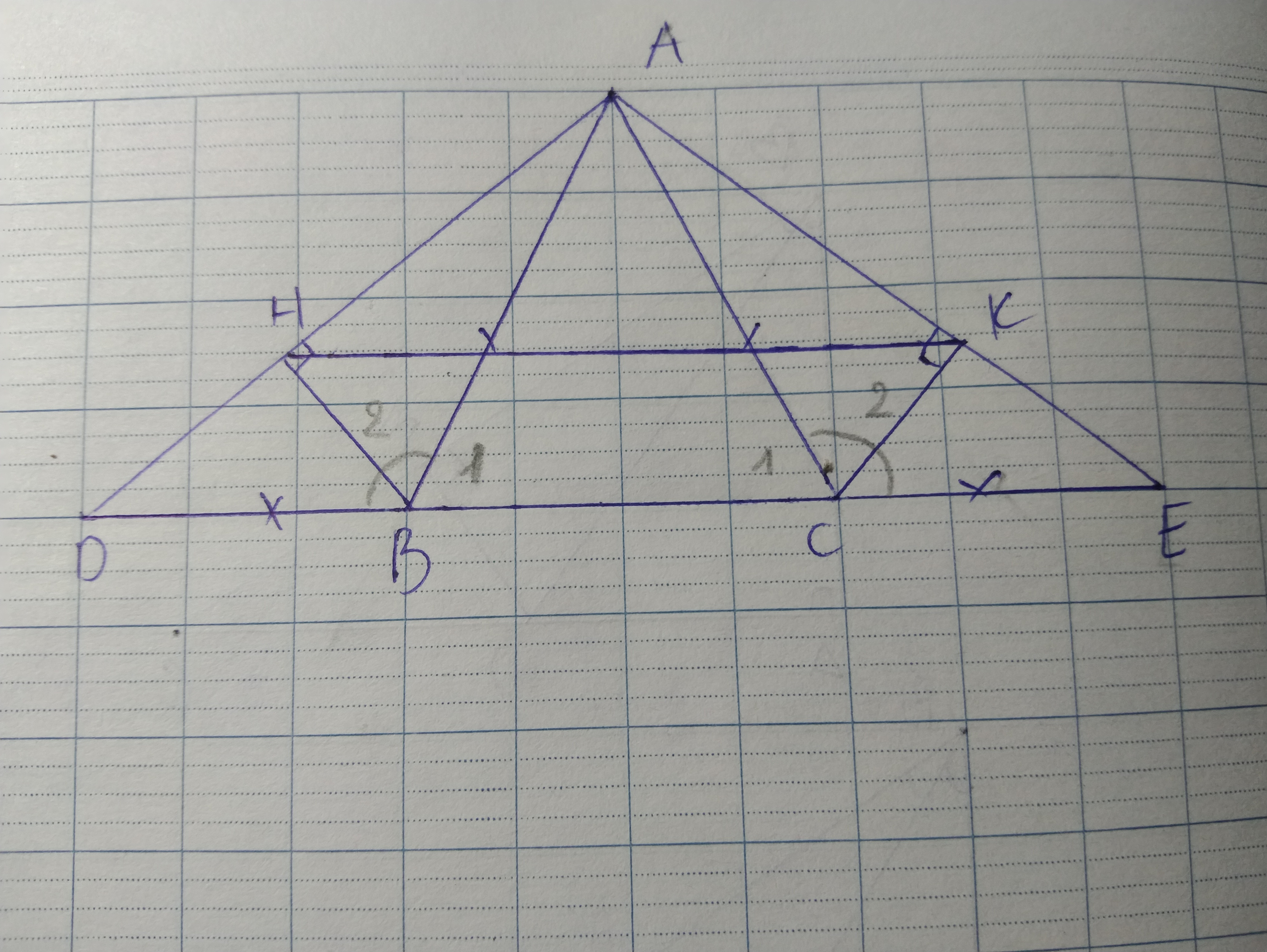
a.
Ta có:
• ^ B1 + ^ B2 = 180⁰ (kề bù)
• ^C1 + ^ C2 = 180⁰ ( kề bù)
Mà: ^B1 = ^C1 ( ∆ ABC cân tại A
=> ^B2 = ^ C2
Xét ∆ BHD và ∆ CKE, ta có:
AB = AC ( ∆ ABC CÂN TẠI A )
^ B2 = ^ C2 (cmt)
BD = CE ( gt)
=> ∆ BHD = ∆ CKE ( c.g.c)
b.
Xét ∆ ABH vuông tại H và ∆ ACK vuông tại K, có:
AB = AC ( ∆ ABC CÂN TẠI A )
HB = KC ( ∆ BHD = CKE)
=> ∆ ABH = ∆ ACK ( cạnh huyền - cạnh góc vuông)
c.
Vì ∆ ABH = ∆ ACK ( câu b)
=> ∆ AHK cân tại A
=> ^ H = 180° -Â : 2 (*)
Ta lại có:
∆ ABC cân tại A
=> ^B1 = 180⁰ - Â : 2 (**)
Từ (*) và (**) ta suy ra : ^ H = ^ B1
Mà ta thấy: ^H và ^ B1 ở vị trí đồng vị
=>
BC // HK
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


