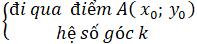A. Phương pháp giải

+ Đường thẳng (d): 

⇒ Phương trình hệ số góc của (d): y= k(x - x₀) + y₀

B. Ví dụ minh họa

Ví dụ 1: Viết phương trình đường thẳng d biết điểm A(2; 1) thuộc đường thẳng d và đường thẳng d tạo với trục x’Ox một góc 45⁰.

A. y = - x + 3    B. y = x + 1    C. y = x - 3 hoặc y = x + 1    D. y = x - 1 hoặc y = - x + 3

Lời giải

+ Do đường thẳng d tạo với trục x’Ox một góc 45⁰ nên hệ số góc của đường thẳng d là k = tan45⁰ = 1 hoặc k = tan135⁰ = - 1

+ Nếu k = 1 thì đường thẳng (d) cần tìm là: y = 1.(x - 2) + 1 hay y = x - 1

+ Nếu k = -1 thì đường thẳng (d) cần tìm là: y = -1(x - 2)+ 1 hay y = - x + 3

Vậy có hai đường thẳng thỏa mãn là: (d₁) y = x - 1 và (d₂): y = - x + 3

Chọn D.

Ví dụ 2: Viết phương trình đường thẳng ∆ biết ∆ đi qua điểm M(2; -5) và có hệ số góc    k = -2.

A. y = - 2x - 1    B. y = - 2x - 9.    C. y = 2x - 1    D. y = 2x - 9

Lời giải

Phương trình đường thẳng có hệ số góc k = -2 nên đường thẳng có dạng: y = - 2x + c

Do điểm M(2; -5) thuộc đường thẳng ∆ nên : -5 = - 2.2 + c ⇔ c= -1.

Vậy phương trình ∆: y= - 2x - 1 .

Chọn A.

Ví dụ 3: Viết phương trình đường thẳng d biết điểm A(1; -1) thuộc đường thẳng d và đường thẳng d tạo với trục x’Ox một góc 60⁰.

A. y = 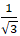 (x-1)- 1

B. y = - √3(x - 1)

C. y = √3(x - 1) - 1 hoặc y = - 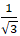 (x - 1) - 1

D. y = √3(x - 1) - 1 hoặc y = - √3(x - 1) - 1

Lời giải

+ Do đường thẳng d tạo với trục x’Ox một góc 60⁰ nên hệ số góc của đường thẳng d là    k = tan60⁰ = √3 hoặc k = tan120⁰ = - √3

+ Nếu k = √3 thì đường thẳng (d) cần tìm là: y = √3(x - 1) - 1.

+ Nếu k = - √3 thì đường thẳng (d) cần tìm là: y = - √3(x - 1) - 1.

Vậy có hai đường thẳng thỏa mãn là: (d₁) y = √3(x - 1) - 1 và (d₂): y = - √3(x - 1) - 1.

Chọn D.

Ví dụ 4: Viết phương trình tổng quát của đường thẳng ∆ biết ∆ đi qua điểm M( -3; -9) và có hệ số góc k = 2

A. x - 2y - 15 = 0    B. 2x + y + 15 = 0    C. 2x - y + 5 = 0    D. 2x - y - 3 = 0

Lời giải

Phương trình đường thẳng có hệ số góc k= 2 nên đường thẳng có dạng: y = 2x + c

Do điểm M(-3; -9) thuộc đường thẳng ∆ nên : - 9 = 2.(-3) + c ⇔ c= - 3

Vậy phương trình ∆: y = 2x - 3 hay 2x - y - 3 = 0

Chọn D.

Ví dụ 5: Viết phương trình đường thẳng biết đi qua điểm M(1; 0) và có hệ số góc k = -1.

A. y= - x + 1    B. y = - x - 9.    C. y = x - 1    D. y = - x - 1

Lời giải

Phương trình đường thẳng có hệ số góc k = -1 nên đường thẳng có dạng: y= - x + c

Do điểm M(1; 0) thuộc đường thẳng ∆ nên : 0 = -1 + c ⇔ c= 1.

Vậy phương trình ∆: y = - x + 1 .

Chọn A.

Ví dụ 6: Viết phương trình tổng quát của đường thẳng ∆ biết ∆ đi qua điểm M( -1; 2) và có hệ số góc k = 3.

A. 3x - y - 1 = 0    B. 3x - y - 5 = 0    C. x - 3y + 5 = 0    D. 3x - y + 5 = 0

Lời giải

Phương trình đường thẳng ∆ có hệ số góc k = 3 nên đường thẳng có dạng: y= 3x + c

Do điểm M(-1;2) thuộc đường thẳng ∆ nên : 2 = 3.(-1) + c ⇔ c= 5.

Vậy phương trình ∆: y = 3x + 5 hay 3x - y + 5 = 0

Chọn D.