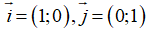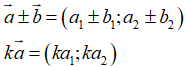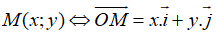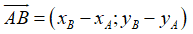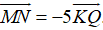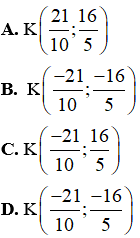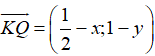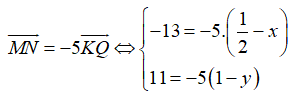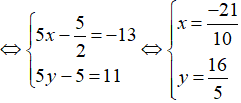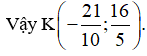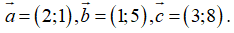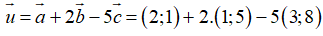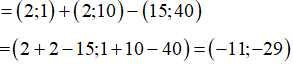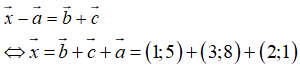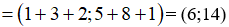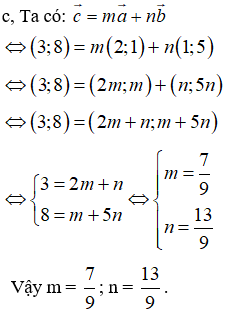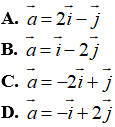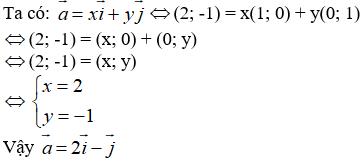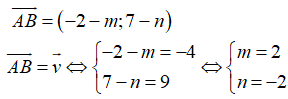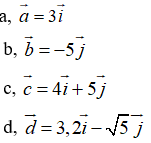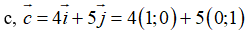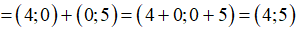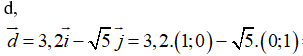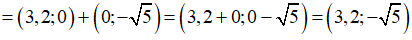Bài tập Tọa độ của vecto, tọa độ của một điểm cực hay, chi tiết
Bài tập Tọa độ của vecto, tọa độ của một điểm cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Bài tập Tọa độ của vecto, tọa độ của một điểm cực hay, chi tiết
Bài tập Tọa độ của vecto, tọa độ của một điểm cực hay, chi tiết
A. Phương pháp giải
Để làm dạng bài tập này, ta phải nắm vững công thức tọa độ vecto, tọa độ của một điểm và mối liên hệ giữa tọa độ điểm và tọa độ vecto.
Tọa độ của vecto:
là các vecto đơn vị, 
Hai vecto bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau. Nếu có 
thì 
.
Cho hai vecto 
. Khi đó ta có
Tọa độ của điểm: Trong mặt phẳng tọa độ Oxy, tọa độ của vecto 
được gọi là tọa độ điểm M
Mối liên hệ: Cho hai điểm A(xA; yA), B(xB; yB). Khi đó ta có
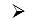
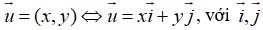
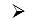
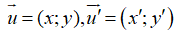
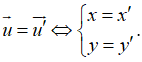
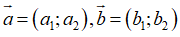
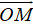
B. Ví dụ minh họa
Ví dụ 1: Ví dụ 5. Trong hệ trục tọa độ Oxy, cho tọa độ các điểm M(3; -6); N(-10; 5) và Q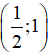
. Tìm tọa độ điểm K để 
Hướng dẫn giải:
Ta có: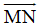 
= (-10 - 3,5 - (-6)) = (-13; 11)
Gọi tọa độ điểm K(x; y). Khi đó ta có 
Đáp án C
Ví dụ 2: Cho 
a, Tìm tọa độ của vecto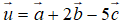 
.
b, Tìm tọa độ vecto sao cho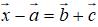 
.
c, Tìm các số m, n để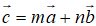 
.
Hướng dẫn giải:
Ta có:
Ví dụ 3: Vecto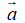 
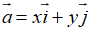
= (2; -1) biểu diễn dưới dạng 
được kết quả nào sau đây?
Hướng dẫn giải:
Đáp án A
Ví dụ 4: Ví dụ 4. Trong hệ trục tọa độ Oxy, cho các điểm A(m; n), B(-2; 7) và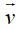 
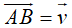
= (-4; 9). Giá trị của m và n để 
.
A. m = -2 và n = 2
B. m = 2 và n = -2
C. m = -6 và n = 16
D. m= 6 và n = -16
Hướng dẫn giải:
Ta có:
Đáp án B
Ví dụ 5: Tìm tọa độ các vecto sau:
Hướng dẫn giải:
Bài viết liên quan
- Bài tập về Quy tắc trọng tâm tam giác của vecto cực hay, chi tiết
- Cách phân tích một vecto theo hai vecto không cùng phương cực hay, chi tiết
- Tìm m để hai vecto cùng phương cực hay, chi tiết
- Cách tìm tọa độ trung điểm của đoạn thẳng cực hay, chi tiết
- Cách tìm tọa độ của trọng tâm tam giác cực hay, chi tiết
