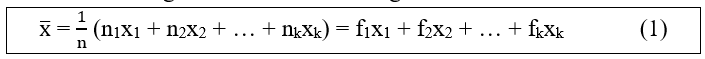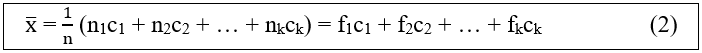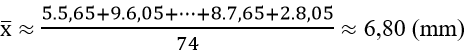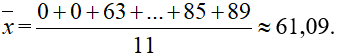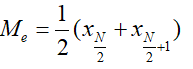Lý thuyết Số trung bình cộng. Số trung vị. Mốt hay, chi tiết
Lý thuyết Số trung bình cộng. Số trung vị. Mốt hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Lý thuyết Số trung bình cộng. Số trung vị. Mốt hay, chi tiết
Lý thuyết Số trung bình cộng. Số trung vị. Mốt hay, chi tiết
Để thu được thông tin quan trọng từ các số liệu thống kê, người ta sử dụng những số đặc trưng như: số trung bình cộng, số trung vị, mốt, phương sai, dộ lệch chuẩn. Các số đạc trưng này phản ánh những khía cạnh khác nhau của dấu hiệu điều tra.
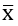
Bảng phân bố tần suất và tần số
| Tên dữ liệu | Tần số | Tần suất (%) |
|
x1 x2 . xk |
n1 n2 . nk |
f1 f2 . fk |
| Cộng | n = n1 + … + nk | 100% |
Trung bình cộng của các số liệu thống kê được tính theo công thức:
Trường hợp Bảng phân bố tần suất và tần số ghép lớp
ci, fi, ni là giá trị đại diện của lớp thứ i.
Ý nghĩa của số trung bình:
Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đặc trưng quan trọng của mẫu số liệu.
Ví dụ 1: Một nhà thực vật học đo chiều dài của 74 chiếc lá cây và thu được số liệu sau ( đơn vị mm)
| Lớp | Giá trị đại diện | Tần số |
|
[5,45 ; 5,85) [5,85 ; 6,25) [6,25 ; 6,65) [6,65 ; 7,05) [7,05 ; 7,45) [7,45 ; 7,85) [7,85 ; 8,25) |
5,65 6,05 6,45 6,85 7,25 7,65 8,05 |
5 9 15 19 16 8 2 |
| N = 74 |
Khi đó chiều dài trung bình của 74 chiếc lá này là :
Ví dụ 2: Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp đến cao như sau: (thang điểm 100): 0 ; 0 ; 63 ; 65 ; 69 ; 70 ; 72 ; 78 ; 81 ; 85 ; 89.
Điểm trung bình là:
Quan sát dãy điểm trên, ta thấy hầu hết (9 em) trong nhóm có số điểm vượt điểm trung bình. Như vậy, điểm trung bình này không phản ứng đúng trình độ trung bình của nhóm.

2. Số trung vị:Kí hiệu: Me
Khi các số liệu trong mẫu có sự chênh lệnh rất lớn đối với nhau thì số trung bình khó có thể đại diện cho các số liệu trong mẫu. Có một chỉ số khác thích hợp hơn trong trường hợp này. Đó là số trung vị.
Định nghĩa: Giả sử ta có dãy n số liệu được sắp xếp thành dãy không giảm (hoặc không tăng). Khi đó, số trung vị (của các số liệu thống kê đã cho) kí hiệu là Me là :
+ Số đứng giữa dãy nếu số phần tử N lẻ: Me =
+ Trung bình cộng của hai số đứng giữa dãy nếu số phần tử N chẵn:
Ví dụ 1: Điểm thi toán của 9 học sinh như sau: 1; 1; 3; 6; 7; 8; 8; 9; 10
Ta có Me = 7
Ví dụ 2: Số điểm thi toán của 4 học sinh như sau: 1; 2,5; 8; 9,5
Ta có Me = 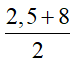
3. Mốt: Kí hiệu: Mo
Mốt của bảng phân bố tần số là giá trị (xi) có tần số (ni ) lớn nhất và được kí hiệu là Mo.
Chú ý: Có hai giá trị tần số bằng nhau và lớn hơn tần số các giá trị khác thì ta nói trường hợp này có hai Mốt, kí hiệu Mo1,Mo2 .
| Giá tiền | 100 | 150 | 300 | 350 | 400 | 500 |
| Số quạt bán được | 256 | 353 | 534 | 300 | 534 | 175 |
Mốt Mo = 300
4. Chọn đại diện cho các số liệu thống kê:
a) Trường hợp các số liệu thông kê cùng loại và số lượng thống kê đủ lớn (n ≥ 30) thì ta ưu tiên chọn số trung bình làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).
b) Trường hợp không tính được giá trị trung bình thì ta chọn số trung vị hoặc mốt làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).
c) Không nên dùng số trung bình để đại diện cho các số liệu thống kê trong các trường hợp sau (có thể dùng số trung vị hoặc mốt):
+ Số các số liệu thống kê quá ít (n ≤ 10).
+ Giữa các số liệu thống kê có sự chênh lệc quá lớn.
+ Đường gấp khúc tần suất không đối xứng, (và nhiều trường hợp khác)