Lý thuyết Bảng phân bố tần số và tần suất hay, chi tiết
Lý thuyết Bảng phân bố tần số và tần suất hay, chi tiết
Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Lý thuyết Bảng phân bố tần số và tần suất hay, chi tiết
Lý thuyết Bảng phân bố tần số và tần suất hay, chi tiết
1. Một số khái niệm cơ bản:
+) Số phần tử của một mẫu được gọi là kích thước mẫu.
+) Các giá trị của dấu hiệu thu được trên mẫu được gọi là một mẫu số liệu.
Chú ý:Khi thực hiện điều tra thống kê (theo mục đích định trước), cần xác định tập hợp các đơn vị điều tra, dấu hiệu điều tra và thu thập các số liệu.
Ví dụ: Số liệu thông kê điểm kiểm tra môn toán của lớp 10A
2. Định nghĩa:
Giả sử dãy n số liệu thống kê đã cho có k giá trị khác nhau (k ≤ n). Gọi xi là một giá trị bất kì trong k giá trị đó, ta có:
Tần số: số lần xuất hiện giá trị xi trong dãy số liệu đã cho gọi là tần số của giá trị đó, kí hiệu là ni.
Ví dụ: Trong bảng số liệu trên ta thấy có 7 giá trị khác nhau là
x1 = 4, x2 = 5, x3 = 6, x4 = 7, x5 = 8, x6 = 9, x7 = 10
x1 = 4 xuất hiện 3 lần => n1 = 3 (tần số của x1 là 3)
Tần suất: Số fi =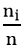 
được gọi là tần suất của giá trị xi (tỉ lệ của ni, tỉ lệ phần trăm)
Ví dụ: x1 có tần số là 3, do đó: f1 =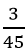 
hay f1 = 5%
3. Bảng phân bố tần suất và tần số
| Tên dữ liệu | Tần số | Tần suất (%) |
|
x1 x2 . . xk |
n1 n2 . . nk |
f1 f2 . . fk |
| Cộng | n1+…+nk | 100% |
Ví dụ:Bảng phân bố tần số và tần suất điểm kiểm tra 15’ môn toán 10CB
| Điểm toán | Tần số | Tần suất ( %) |
|
4 5 6 7 8 9 10 |
3 7 11 9 6 7 2 |
6,67 15,56 24,44 20 13,33 15,6 4,4 |
| Cộng | 45 | 100% |
Chú ý: Nếu bỏ cột tầng số thì ta được bảng phân bố tần suất; bỏ cột tần suất thì ta được bảng phân bố tần số.
4. Bảng phân bố tần số và tần suất ghép lớp
Giả sử p dãy số liệu thông kê đã cho được phân vào k lớp (k < n). Xét lớp thứ i trong k lớp đó, ta có:
Số ni các số liệu thông kê thuộc lớp thứ i được tần số của lớp đó.
Số fi =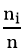 
được gọi là tần số của lớp thứ i
| Lớp điểm toán | Tần số | Tần suất ( %) |
|
[4;7] [7;9] [9;10] |
21 15 9 |
46,67 33,33 20 |
| Cộng | 45 | 100% |
Bảng này gọi là bảng phân bố tần số và tần suất ghép lớp. Nếu bỏ cột tần số thì ta được bảng phân bố tần suất ghép lớp; Nếu bỏ cột tần suất thì ta được bảng phân bố tần số ghép lớp.
