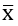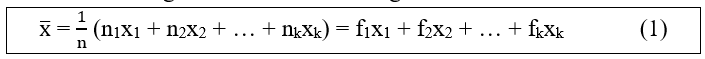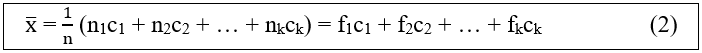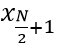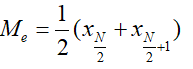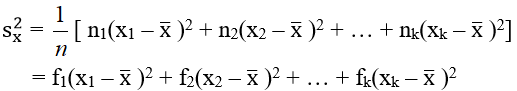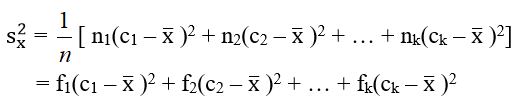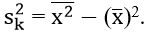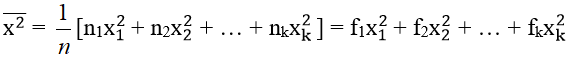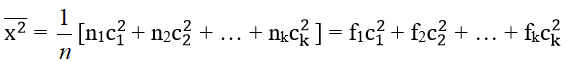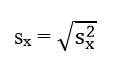Lý thuyết tổng hợp chương Thống kê hay, chi tiết
Lý thuyết tổng hợp chương Thống kê hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Lý thuyết tổng hợp chương Thống kê hay, chi tiết
Lý thuyết tổng hợp chương Thống kê hay, chi tiết
1. Một số khái niệm cơ bản:
• Một tập con hữu hạn các đơn vị điều tra được gọi là một mẫu.
• Số phần tử của một mẫu được gọi là kích thước mẫu.
• Các giá trị của dấu hiệu thu được trên mẫu được gọi là một mẫu số liệu.
Chú ý:Khi thực hiện điều tra thống kê (theo mục đích định trước), cần xác định tập hợp các đơn vị điều tra, dấu hiệu điều tra và thu thập các số liệu.

Ví dụ: Số liệu thông kê điểm kiểm tra môn toán của lớp 10A
2. Định nghĩa:
Giả sử dãy n số liệu thống kê đã cho có k giá trị khác nhau (k ≤ n). Gọi xi là một giá trị bất kì trong k giá trị đó, ta có:
Tần số: số lần xuất hiện giá trị xi trong dãy số liệu đã cho gọi là tần số của giá trị đó, kí hiệu là ni.
x1 = 4, x2 = 5, x3 = 6, x4 = 7, x5 = 8, x6 = 9, x7 = 10
x1 = 4 xuất hiện 3 lần => n1 = 3 (tần số của x1 là 3)
Tần suất: Số fi = 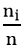
Ví dụ: x1 có tần số là 3, do đó: f1 = 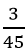
3. Bảng phân bố tần suất và tần số
| Tên dữ liệu | Tần số | Tần suất (%) |
|
x1 x2 . . xk |
n1 n2 . . nk |
f1 f2 . . fk |
| Cộng | n1+…+nk | 100% |
Chú ý: Nếu bỏ cột tầng số thì ta được bảng phân bố tần suất; bỏ cột tần suất thì ta được bảng phân bố tần số.
4. Bảng phân bố tần số và tần suất ghép lớp
Giả sử p dãy số liệu thông kê đã cho được phân vào k lớp (k < n). Xét lớp thứ i trong k lớp đó, ta có:
Số ni các số liệu thông kê thuộc lớp thứ i được tần số của lớp đó.
Số fi = 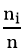
BIỂU ĐỒ
1.Biểu đồ tần suất hình cột:
Cách vẽ:
• Vẽ hai đường thẳng vuông góc. Trên đường thẳng nằm ngang (dùng làm trục số) ta đánh dáu các khoảng xác định lớp.
• Tại mỗi khoảng ta dựng lên một hình cột chữ nhật, với đáy là khoảng đó, còn chiều cao bằng tần suất của lớp mà khoảng đó xác định
2. Đường gấp khúc tần suất
Cách vẽ: Ta vẽ hai đường thẳng vuông góc ( như hình vễ biểu đồ hình cột). Trên mặt phẳng tọa độ xác định các điểm (ci+1; fi+1), i = 1, 2, 3,…, n sau đó vẽ các đoạn thẳng nối các điểm (ci, fi) với các điểm (ci+1; fi+1), i = 1, 2, 3,…, n ta thu được một đường gấp khúc. Đường gấp khúc này gọi là đường gấp khúc tần suất.
3. Biểu đồ hình quạt:
Cách vẽ: vẽ hình tròn, chia hình tròn thành những hình quạt, mỗi lớp tương ứng với một hình quạt mà diện tích của nó tỉ lệ với tần suất của lớp đó.
SỐ TRUNG BÌNH CỘNG. SỐ TRUNG VỊ. MỐT
1. Số trung bình cộng : Kí hiệu:
Bảng phân bố tần suất và tần số
| Tên dữ liệu | Tần số | Tần suất (%) |
|
x1 x2 . xk |
n1 n2 . nk |
f1 f2 . fk |
| Cộng | n = n1 + … + nk | 100% |
Trung bình cộng của các số liệu thống kê được tính theo công thức:
Trường hợp Bảng phân bố tần suất và tần số ghép lớp
ci, fi, ni là giá trị đại diện của lớp thứ i.
Ý nghĩa của số trung bình:
Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đặc trưng quan trọng của mẫu số liệu.
2. Số trung vị:Kí hiệu: Me
Khi các số liệu trong mẫu có sự chênh lệnh rất lớn đối với nhau thì số trung bình khó có thể đại diện cho các số liệu trong mẫu. Có một chỉ số khác thích hợp hơn trong trường hợp này. Đó là số trung vị.
Định nghĩa: Giả sử ta có dãy n số liệu được sắp xếp thành dãy không giảm (hoặc không tăng). Khi đó, số trung vị (của các số liệu thống kê đã cho) kí hiệu là Me là :
+ Số đứng giữa dãy nếu số phần tử N lẻ: Me =
+ Trung bình cộng của hai số đứng giữa dãy nếu số phần tử N chẵn:
3. Mốt: Kí hiệu: Mo
Mốt của bảng phân bố tần số là giá trị (xi) có tần số (ni ) lớn nhất và được kí hiệu là Mo.
Chú ý: Có hai giá trị tần số bằng nhau và lớn hơn tần số các giá trị khác thì ta nói trường hợp này có hai Mốt, kí hiệu Mo1,Mo2 .
4. Chọn đại diện cho các số liệu thống kê:
a) Trường hợp các số liệu thông kê cùng loại và số lượng thống kê đủ lớn (n ≥ 30) thì ta ưu tiên chọn số trung bình làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).
b) Trường hợp không tính được giá trị trung bình thì ta chọn số trung vị hoặc mốt làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).
c) Không nên dùng số trung bình để đại diện cho các số liệu thống kê trong các trường hợp sau (có thể dùng số trung vị hoặc mốt):
+ Số các số liệu thống kê quá ít (n ≤ 10).
+ Giữa các số liệu thống kê có sự chênh lệc quá lớn.
+ Đường gấp khúc tần suất không đối xứng, (và nhiều trường hợp khác)
PHƯƠNG SAI. ĐỘ LỆCH CHUẨN
1. Phương sai: Kí hiệu sx2
Trường hợp bảng phân bố tần số, tần suất
Trường hợp bảng phân bố tần số, tần suất ghép lớp
Trong đó lần lượt là tần số, tần suất, giái trị đại diện của lớp thứ i; n là số các số liệu thống kê; là số trung bình cộng của các số liệu thống kê đã cho
Chú ý:Có thể tính theo công thức sau:
Trong đó
(đối với bảng phân bố tần số, tần suất)
hoặc
(đối với bảng phân bố tần số, tần suất ghép lớp)
Ý nghĩa phương sai
Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
Khi hai dãy số liệu thống kê có cùng đơn vị đo và có số trung bình bằng nhau hoặc xấp xỉ nhau, dãy có phương sai càng nhỏ thì mức độ phân tán (so với số trung bình) của các số liệu thống kê càng bé.
2. Độ lệch chuẩn:
Khi chú ý đơn vị đo ta thấy phương sai sx2 có đơn vị đo là bình phương của đơn vị đo được nghiên cứu ( đơn vị đo nghiên cứu là cm thì sx2 là cm2), để tránh tình trạng này ta dùng căn bậc hai của phương sai gọi là độ lệch chuẩn.
Độ lệch chuẩn, kí hiệu là sx
Ý nghĩa độ lệch chuẩn: Độ lệch chuẩn cũng dùng đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình). Khi cần chú ý đến đơn vị đo ta dùng độ lệch chuẩn để đánh giá vì độ lệch chuẩn có cùng đơn vị đó với dấu hiệu X được nghiên cứu.