Lý thuyết Dấu của tam thức bậc hai hay, chi tiết
Lý thuyết Dấu của tam thức bậc hai hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Lý thuyết Dấu của tam thức bậc hai hay, chi tiết
Lý thuyết Dấu của tam thức bậc hai hay, chi tiết
I. ĐỊNH LÍ VỀ DẤU CỦA TAM THỨC BẬC HAI
1. Tam thức bậc hai
Tam thức bậc hai đối với x là biểu thức có dạng
f(x) = ax2 + bx + c,
trong đó a, b, c là những hệ số, a ≠ 0.

2. Dấu của tam thức bậc hai
Người ta đã chứng minh được định lí về dấu tam thức bậc hai sau đây
Định lý
Cho f(x) = ax2 + bx + c (a ≠ 0), Δ = b2 – 4ac.
Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ R.
Nếu Δ = 0 thì f(x) luôn cùng dấu với hệ số a, trừ khi x = -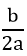
Nếu Δ > 0 thì f(x) luôn cùng dấu với hệ số a khi x < x1 hoặc x > x2, trái dấu với hệ số a khi x1 < x < x2 trong đó x1, x2 (x1 < x2) là hai nghiệm của f(x).
Chú ý
Trong định lí trên, có thể thay biệt thức Δ = b2 – 4ac bằng biệt thức thu gọn Δ’ = (b’)2 – ac
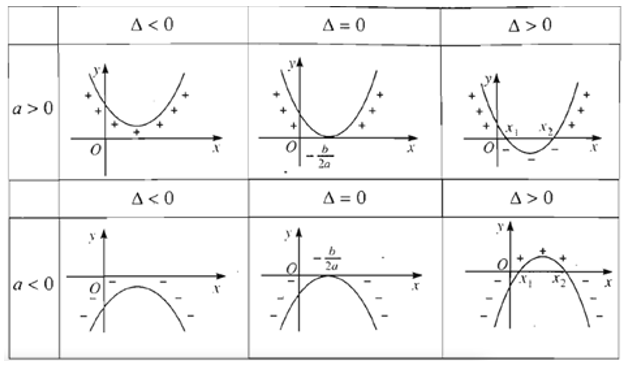
Minh họa hình học
Định lí về dấu của tam thức bậc hai có minh họa hình học sau
II. BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
1. Bất phương trình bậc hai
Bất phương trình bậc hai ẩn x là bất phương trình dạng ax2 + bx + c < 0 (hoặc ax2 + bx + c ≤ 0 , ax2 + bx + c > 0, ax2 + bx + c ≥ 0), trong đó a, b, c là những số thực đã cho, a ≠ 0.
2. Giải bất phương trình bậc hai
Giải bất phương trình bậc hai ax2 + bx + c < 0 thực chất là tìm các khoảng mà trong đó f(x) = ax2 + bx + c cùng dấu với hệ số a (trường hợp a < 0) hay trái dấu với hệ số a (trường hợp a > 0).