Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A
Lời giải Bài 2.29 trang 28 SBT Toán 10 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Bài 2.29 trang 28 SBT Toán 10 Tập 1:Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống I và II.
Mỗi cốc đồ uống I cung cấp 60 calo, 12 đơn vị vitamin A và 10 đơn vị vitamin C.Mỗi cốc đồ uống II cung cấp 60 calo, 6 đơn vị vitamin A và 30 đơn vị vitamin C. Biết rằng một cốc đồ uống I có giá 12 nghìn đồng và một cốc đồ uống II có giá 15 nghìn đồng.
a) Gọi x và y tương ứng là số cốc đồ uống I và II. Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình và xác định miền nghiệm của hệ đó.
b) Gọi F (nghìn đồng) là số tiền phải trả cho x cốc đồ uống I và y cốc đồ uống II. Hãy biểu diễn F theo x và y.
c) Biết rằng F đạt giá trị nhỏ nhất trên miền nghiệm tìm được ở câu a tại một trong các đỉnh của miền nghiệm, tìm giá trị nhỏ nhất đó. Từ đó suy ra người đó cần uống bao nhiêu cốc loại I và loại II để chi phí là nhỏ nhất mà vẫn đáp ứng được yêu cầu hằng ngày.
Lời giải:
a) Do có x cốc đồ uống I và y cốc đồ uống II nên x ≥ 0; y ≥ 0.
x cốc đồ uống I cung cấp 60x calo, 12x đơn vị vitamin A và 10x đơn vị vitamin C.
y cốc đồ uống II cung cấp 60y calo, 6y đơn vị vitamin A và 30y đơn vị vitamin C.
Do người đó cần cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C nên 60x + 60y ≥ 300; 12x + 6y ≥ 36; 10x + 30y ≥ 90.
Khi đó ta có hệ bất phương trình sau:
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(3; 3) d1 và thay vào biểu thức x ta được 3 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(3; 3).
• Đường thẳng d2: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(3; 3) d2 và thay vào biểu thức y ta được 3 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d2 chứa điểm I(3; 3).
• Vẽ đường thẳng d3: x + y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; 5) và (5; 0).
Chọn điểm I(3; 3) d3 và thay vào biểu thức x + y ta được 6 > 5.
Suy ra miền nghiệm của bất phương trình x + y ≥ 5 là nửa mặt phẳng bờ d3 chứa điểm I(3; 3).
• Vẽ đường thẳng d4: 2x + y = 6 bằng cách vẽ đường thẳng đi qua hai điểm (0; 6) và (1; 4).
Chọn điểm I(3; 3) d4 và thay vào biểu thức x + y ta được 2 . 3 + 3 = 9 > 6.
Suy ra miền nghiệm của bất phương trình 2x + y ≥ 5 là nửa mặt phẳng bờ d4 chứa điểm I(3; 3).
• Vẽ đường thẳng d5: x + 3y = 9 bằng cách vẽ đường thẳng đi qua hai điểm (0; 3) và (3; 2).
Chọn điểm I(3; 3) d5 và thay vào biểu thức x + 3y ta được 2 + 3 . 3 = 11 > 5.
Suy ra miền nghiệm của bất phương trình x + 3y ≥ 9 là nửa mặt phẳng bờ d5 chứa điểm I(3; 3).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
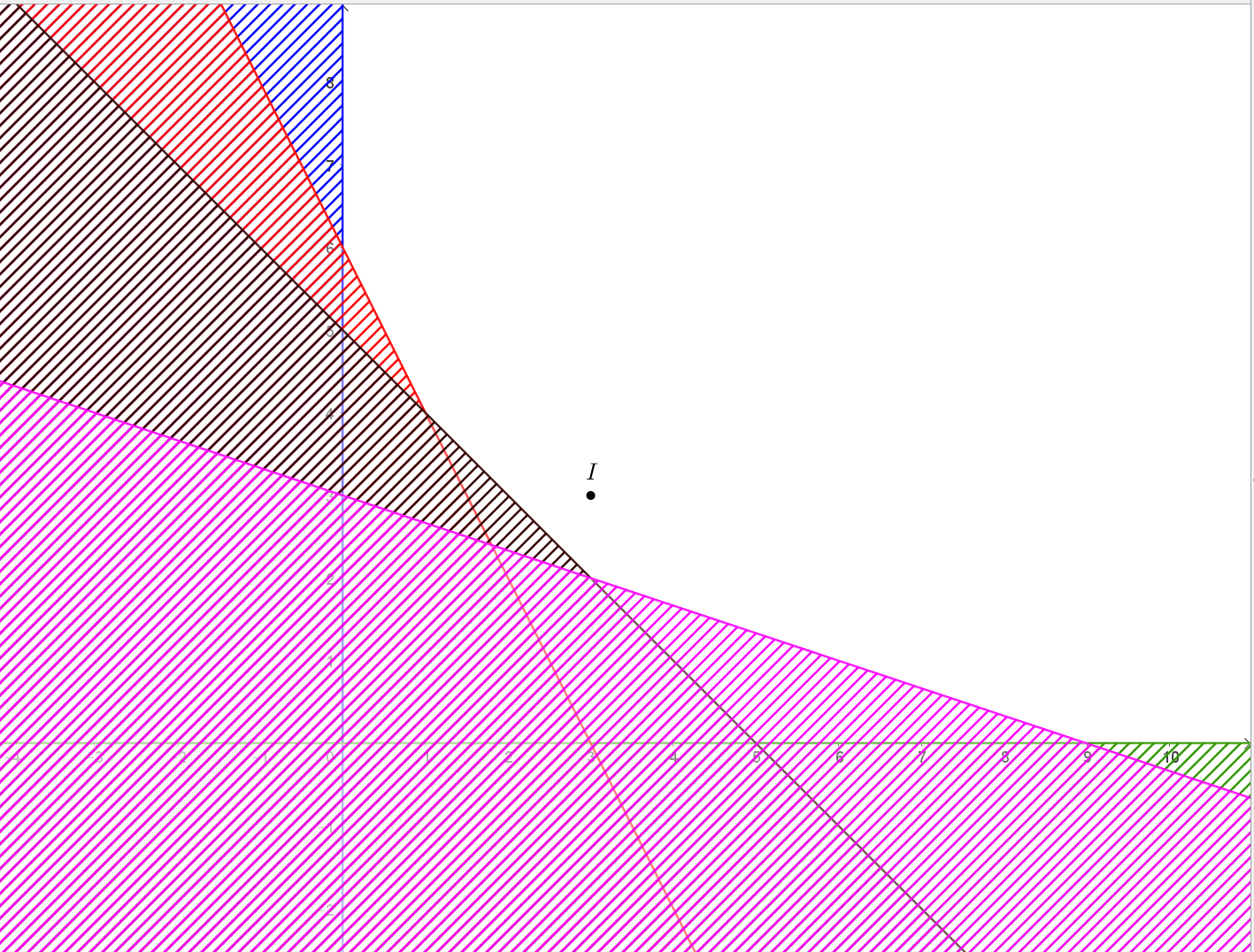
Ta thấy miền nghiệm của hệ bất phương trình trên là miền tứ giác với các đỉnh (0; 6), (1; 4), (3; 2), (9; 0).
b) Chi phí cho hai loại đồ uống là F(x; y) = 12x + 15y (nghìn đồng).
c) Ta có:
F(0; 6) = 12 . 0 + 15 . 6 = 90;
F(1; 4) = 12 . 1 + 15 . 4 = 72;
F(3; 2) = 12 . 3 + 15 . 2 = 66;
F(9; 0) = 12 . 9 + 15 . 0 = 108.
Giá trị nhỏ nhất của F(x; y) bằng 66 khi x = 3 và y = 2.
Vậy người đó cần uống 3 cốc đồ uống I và 2 cốc đồ uống II để đạt được các mục tiêu đã đề ra.
Xem thêm các bài giải sách bài tập Toán 10 bộ sách Kết nối tri thức hay, chi tiết khác:
Bài 2.15 trang 25 SBT Toán 10 Tập 1: Cặp số nào dưới đây là nghiệm của hệ bất phương trình ?...
Bài 2.18 trang 26 SBT Toán 10 Tập 1: Miền nghiệm của hệ bất phương trình 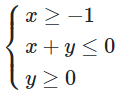 là...
là...
Bài 2.19 trang 26 SBT Toán 10 Tập 1: Miền nghiệm của bất phương trình là...
Bài 2.20 trang 26 SBT Toán 10 Tập 1: Miền nghiệm của hệ bất phương trình là...


