Giải sách bài tập Toán lớp 7 Bài 2: Làm quen với xác xuất của biến cố ngẫu nhiên

Bài 1 trang 85 SBT Toán 7 Tập 2: Gieo một con xúc xắc 6 mặt cân đối. Tính xác suất của các biến cố sau.

A: “Xuất hiện mặt có 2 chấm”;

B: “Xuất hiện mặt có số chấm chia hết cho 4”;

C: “Xuất hiện mặt có số chấm chia hết cho 7”;

D: “Xuất hiện mặt có số chấm là ước của 60”.

Lời giải

• Vì con xúc xắc cân đối nên khả năng xuất hiện các mặt của nó như nhau.

Do đó $P\left(A\right)=\frac{1}{6}$.

• Chỉ có mặt 4 chấm là số chia hết cho 4. Do đó $P\left(B\right)=\frac{1}{6}$.

• Vì không có mặt nào xuất hiện số chấm chia hết cho 7 nên C là biến cố không thể, do đó P(C) = 0.

• Vì số chấm của cả 6 mặt con xúc xắc (1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm) đều là ước của 60 nên D là biến cố chắc chắn, do đó P(D) = 1.

Vậy $P\left(A\right)=\frac{1}{6}$, $P\left(B\right)=\frac{1}{6}$, P(C) = 0 và P(D) = 1.

Bài 2 trang 85 SBT Toán 7 Tập 2: Trên tường có một đĩa hình tròn có cấu tạo đồng chất và cân đối (Hình 3). Mặt đĩa được chia thành 12 hình quạt bằng nhau và được đánh số từ 1 đến 12. Hoàng quay đĩa quanh trục gắn ở tâm và quan sát xem khi dừng lại mũi tên chỉ vào ô số mấy. Tính xác suất của các biến cố sau:

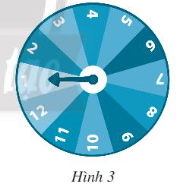
A: “Mũi tên chỉ vào ô số 7”;

B: “Mũi tên chỉ vào ô ghi số lẻ”;

C: “Mũi tên chỉ vào ô ghi số lớn hơn 11”.

Lời giải

• Vì đĩa hình tròn có cấu tạo đồng chất và cân đối, chia thành 12 hình quạt bằng nhau nên khả năng mũi tên chỉ vào các hình quạt là như nhau.

Do đó xác suất xảy ra biến cố A là $P\left(A\right)=\frac{1}{12}$.

• Do phần các hình quạt ghi số chẵn có kích thước bằng phần các hình quạt ghi số lẻ nên xác suất xảy ra của biến cố B là $P\left(B\right)=\frac{1}{2}$.

• Do các hình quạt có kích thước bằng nhau nên mũi tên chỉ vào hình quạt ghi số 12 (là ô duy nhất ghi số lớn hơn 11), do đó xác suất xảy ra biến cố của C là $P\left(C\right)=\frac{1}{12}$.

Vậy $P\left(A\right)=\frac{1}{12}$, $P\left(B\right)=\frac{1}{2}$ và $P\left(C\right)=\frac{1}{12}$.

Bài 3 trang 85 SBT Toán 7 Tập 2: Một chiếc hộp kín có chứa 5 quả bóng có kích thước và khối lượng như nhau, và được ghi lần lượt các số 5, 10, 15, 20, 25. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất của các biến cố sau.

A: “Quả bóng lấy ra được ghi số nguyên tố”;

B: “Quả bóng lấy ra ghi số chia hết cho 5”;

C: “Quả bóng lấy ra ghi số chia hết cho 3”;

D: “Quả bóng lấy ra ghi số là bội của 6”.

Lời giải

Vì 5 quả bóng có kích thước và khối lượng như nhau nên mỗi quả bóng đều có cùng khả năng được chọn.

• Trong 5 quả bóng ghi lần lượt các số 5, 10, 15, 20, 25, chỉ có 1 quả bóng ghi số nguyên tố là 5. Do đó xác xuất của biến cố A là $P\left(A\right)=\frac{1}{5}$.

• Tất cả 5 quả bóng ghi lần lượt các số 5, 10, 15, 20, 25 đều là số chia hết cho 5 vì đều có tận cùng là 0 hoặc 5. Do đó biến cố B là biến cố chắc chắn nên xác suất của biến cố B là P(B) = 1.

• Trong 5 quả bóng ghi lần lượt các số 5, 10, 15, 20, 25, chỉ có quả bóng được ghi số 15 là số chia hết cho 3. Do đó xác suất của biến cố C là $P\left(C\right)=\frac{1}{5}$.

• Trong 5 quả bóng ghi lần lượt các số 5, 10, 15, 20, 25, không có quả bóng nào ghi số là bội của 6 nên biến cố D là biến cố không thể. Do đó, xác suất của biến cố D là P(D) = 0.

Vậy $P\left(A\right)=\frac{1}{5}$, P(B) = 1, $P\left(C\right)=\frac{1}{5}$ và P(D) = 0.

Bài 4 trang 86 SBT Toán 7 Tập 2: Một chiếc hộp kín có chứa 5 quả bóng màu xanh, 5 quả bóng màu đỏ và 5 quả bóng màu trắng có kích thước và khối lượng như nhau. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất của biến cố bóng lấy ra có màu xanh.

Lời giải

Gọi A: “Quả bóng lấy ra có màu xanh”.

Cách 1:

Vì các quả bóng có kích thước và khối lượng như nhau nên các quả bóng đều có cùng khả năng được lấy ra.

Do có 5 quả bóng màu xanh trong tổng số 5 + 5 + 5 = 15 quả bóng nên xác suất của biến cố A: “Quả bóng lấy ra có màu xanh” là $\frac{5}{15}=\frac{1}{3}.$

Cách 2:

Do số quả bóng màu xanh, đỏ, trắng là bằng nhau và các quả bóng đều có cùng kích thước, khối lượng nên cả 3 màu đều có cùng khả năng được chọn.

Do đó xác suất của biến cố biến cố A: “Quả bóng lấy ra có màu xanh” là $\frac{1}{3}$.

Vậy xác suất của biến cố bóng lấy ra có màu xanh là $\frac{1}{3}$.

Bài 5 trang 86 SBT Toán 7 Tập 2: Trong hộp có 1 viên bi màu xanh, 1 viên bi màu trắng và 1 viên bi màu đỏ có kích thước và trọng lượng như nhau. Lấy ra ngẫu nhiên 2 viên bi từ hộp. Tính xác suất của các biến cố sau

A: “Hai viên bi lấy ra có cùng màu”

B: “Không có viên bi nào có màu xanh hay trắng trong hai viên bi được chọn”

Lời giải

‒ Vì trong hộp chỉ có 1 viên bi màu xanh, 1 viên bi màu trắng và 1 viên bi màu đỏ có kích thước và trọng lượng như nhau nên không thể có khả năng lấy ra ngẫu nhiên 2 viên bi có cùng màu.

Do đó biến cố A là biến cố không thể.

Khi đó xác suất của biến cố A là P(A) = 0.

‒ Vì lấy ngẫu nhiên 2 viên bi nên sẽ có các khả năng xảy ra đối với màu của hai viên bi như sau:

• 1 viên bi màu xanh và 1 viên bi màu trắng.

• 1 viên bi màu xanh và 1 viên bi màu đỏ;

• 1 viên bi màu trắng và một viên bi màu đỏ.

Do đó biến cố B là biến cố không thể.

Khi đó, xác suất của biến cố B là P(B) = 0.

Vậy P(A) = 0 và P(B) = 0.

Bài 6 trang 86 SBT Toán 7 Tập 2: Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020. Chọn ngẫu nhiên 1 năm trong 6 năm đó. Tính xác suất của các biến cố sau.

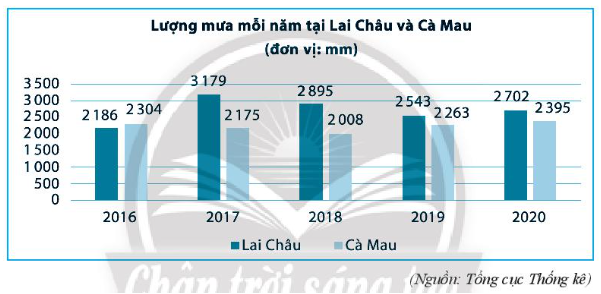
A: “Tại năm được chọn lượng mưa ở Cà Mau cao hơn ở Lai Châu”;

B: “Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m”;

C: “Tại năm được chọn, lượng mưa ở Lai Châu gấp hai lần lượng mưa ở Cà Mau”.

Lời giải

+ Quan sát biểu đồ trên thấy có 1 năm mà lượng mưa ở Cà Mau cao hơn lượng mưa ở Lai Châu là: năm 2016;

Vì chọn ngẫu nhiên một năm nên xác suất của biến cố A: “Tại năm được chọn lượng mưa ở Cà Mau cao hơn ở Lai Châu” là P(A) = $\frac{1}{5}$

+ Ta có: 25 m = 25 000 mm.

Quan sát biểu đồ ta thấy tất cả các năm 2016, 2017, 2018, 2019, 2020 đều có lượng mưa ở Cà Mau thấp hơn 25 000 mm.

Do đó biến cố B: “Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m” là biến cố chắc chắn nên P(B) = 1.

+ Quan sát biểu đồ ta dễ dàng thấy rằng không có năm nào lượng mưa ở Lai Châu gấp hai lần lượng mưa ở Cà Mau nên biến cố C là biến cố không thể. Do đó, xác suất của biến cố C là P(C) = 0.

Vậy P(A) = $\frac{1}{5}$, P(B) = 1 và P(C) = 0.

Bài 7 trang 86 SBT Toán 7 Tập 2: Gieo hai đồng xu cân đối và đồng chất. Hãy so sánh xác suất xảy ra của các biến cố sau:

A: “Có không quá hai đồng sấp”;

B: “Cả hai đồng đều sấp”;

C: “Có ít nhất một đồng sấp”.

Lời giải

Vì hai đồng xu cân đối và đồng chất nên khi gieo sẽ có các khả năng xảy ra như sau: 1 đồng sấp, 1 đồng ngửa hoặc cả 2 đồng sấp hoặc cả 2 đồng ngửa.

Khi đó biến cố A: “Có không quá hai đồng sấp” là biến cố chắc chắn, nên P(A) = 1.

Biến cố B và C là biến cố ngẫu nhiên, khi biến cố B: “Cả hai đồng đều sấp” xảy ra thì biến cố C: “Có ít nhất một đồng sấp” cũng xảy ra. Do đó 0 < P(B) < P(C) < 1.

Vậy P(B) < P(C) < P(A).

Bài 8 trang 86 SBT Toán 7 Tập 2: Mật khẩu mở máy tính của Cường gồm 8 kí tự, trong đó 2 kí tự đầu là chữ số, 6 kí tự sau là chữ cái. Không may Cường quên mất kí tự đầu tiên. Cường chọn ra 2 chữ số một cách ngẫu nhiên và thử mở máy tính. Tính xác suất để Cường mở được máy tính.

Lời giải

Do mật khẩu có 2 chữ kí tự đầu là chữ số nên Cường phải chọn ngẫu nhiên 2 chữ số bất kì từ 00 đến 99 để thử mở máy tính.

Mà từ 00 đến 99 có 100 số.

Cường chọn ra một trong 100 số đó một cách ngẫu nhiên và thử mở máy tính nên xác suất để Cường mở được máy tính là $\frac{1}{100}$.