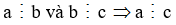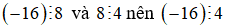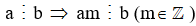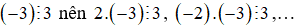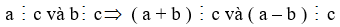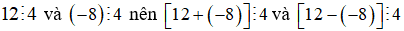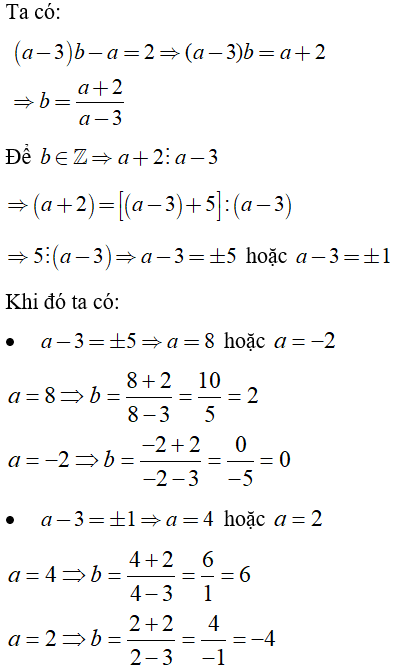Bài 32: Bội và ước của một số nguyên

A. Lý thuyết

1. Bội và ước của một số nguyên

Cho a, b và b . Nếu có số nguyên q sao cho a = bq thì ta nói a chia hết cho b. Ta còn nói a là bội của b và b là ước của a.

Ví dụ: -9 là bội của 3 vì (-9) = 3.(-3)

Chú ý:

• Nếu a = bq (b ≠ 0) thì ta còn nói a chia cho b được q và viết a:b = q.

• Số 0 là bội của mọi số nguyên khác 0.

• Số 0 không phải là ước của bất kì số nguyên nào.

• Các số 1 và -1 là ước của mọi số nguyên.

• Nếu c vừa là ước của a vừa là ước của b thì c cũng được gọi là ước chung của a và b.

Ví dụ:

Các ước của 8 là: -8; -4; -2; -1; 1; 2; 4; 8.

Các bội của 3 là: 0; 3; 6; 9; -3; -6; -9;...

2. Tính chất

• Nếu a chia hết cho b và b chia hết cho c thì a cũng chia hết cho c.

Ví dụ:

• Nếu a chia hết cho b thì bội của a cũng chia hết cho b

Ví dụ:

• Nếu hai số a, b chia hết cho c thì tổng và hiệu của chúng cũng chia hết cho c.

Ví dụ:

3. Ví dụ

Ví dụ 1: Cho tập hợp A = {7; 8; 9; 10} và B = {4; 5; 6}

a) Có thể lập được bao nhiêu dạng tổng a + b với a ∈ A, b ∈ B

b) Tổng trên có bao nhiêu tổng chia hết cho 2

c) Viết tập hợp các phần tử có dạng a.b với a ∈ A, b ∈ B trong tập trên có bao nhiêu phần tử là bội của 5.

Hướng dẫn giải:

a) Ta có:

C = {a + b | a ∈ A, b ∈ B |}

C={11; 12; 13; 14; 15; 16}

b)

Có 3 số chia hết cho 2 là 12, 14, 16

c) Ta có: T = {28; 35; 42; 32; 40; 48; 36; 45; 54; 50; 60}

Trong tập hợp T có các phần tử là bội của 5 là 35; 40; 45; 50; 60

Ví dụ 2: Tìm a, b ∈ ℤ sao (a - 3)b - a = 2

Hướng dẫn giải:

4. Bài tập tự luyện

Câu 1: Tìm các bội của -13 lớn hơn -40 và nhỏ hơn 40

Hướng dẫn giải:

Tập hợp các bội của -13 là {0; -13; 13; -26; 26; -39; 39; -52; 52; ...}

Mà theo bài ta có: bội đó lớn hơn -40 và nhỏ hơn 40

Nên các bội cần tìm là {-39; -26; -13; 0; 13; 26; 39}

Vậy các bội số thỏa mãn yêu cầu là {-39; -26; -13; 0; 13; 26; 39}

Câu 2: Tìm tất cả các ước của -15 và 54

Hướng dẫn giải:

Các ước của -15 là {-15; -5; -3; -1; 1; 3; 5; 15}

Vậy các ước cần tìm là {-15; -5; -3; -1; 1; 3; 5; 15}

Các ước của 54 là {-54; -27; -18; -9; -6; -3; -2; -1; 1; 2; 3; 6; 9; 18; 27; 54}

Vậy các ước cần tìm là {-54; -27; -18; -9; -6; -3; -2; -1; 1; 2; 3; 6; 9; 18; 27; 54}

B. Bài tập trắc nghiệm

Câu 1: Cho a, b ∈ Z và b ≠ 0. Nếu có số nguyên q sao cho a = bq thì:

A. a là ước của b     B. b là ước của a

C. a là bội của b     D. Cả B, C đều đúng

Đáp án

Câu 2: Các bội của 6 là:

A. -6; 6; 0; 23; -23     B. 132; -132; 16

C. -1; 1; 6; -6     D. 0; 6; -6; 12; -12; ...

Đáp án

Câu 3: Tập hợp các ước của -8 là:

A. A = {1; -1; 2; -2; 4; -4; 8; -8}     B. A = {0; ±1; ±2; ±4; ±8}

C. A = {1; 2; 4; 8}     D. A = {0; 1; 2; 4; 8}

Đáp án

Câu 4: Có bao nhiêu ước của -24

A. 9     B. 17     C. 8     D. 16

Đáp án

Câu 5: Tập hợp tất cả các bội của 7 có giá trị tuyệt đối nhỏ hơn 50 là:

A. {0; ±7; ±14; ±21; ±28; ±35; ±42; ±49}

B. {±7; ±14; ±21; ±28; ±35; ±42; ±49}

C. {0; 7; 14; 21;28; 35; 42; 49}

D. {0; 7; 14; 21; 28; 35; 42; 49; -7; -14; -21; -28; -35; -42; -49; -56; ...}

Đáp án

Câu 6: Tìm x, biết 12:x và x < -2

A. {1}     B. {-3; -4; -6; -12}

C. {-2; -1}     D. {-2; -1; 1; 2; 3; ;4; 6; 12}

Đáp án

Câu 7: Trong các khẳng định sau, khẳng định sai là:

A. Số 0 là bội của mọi số nguyên khác 0

B. Số 0 không phải là ước của bất kì số nguyên nào

C. Các số - 1; 1 là ước của mọi số nguyên

D. Nếu a chia hết cho b thì a cũng chia hết cho bội của b

Đáp án

Câu 8: Tìm các số nguyên x thỏa mãn (x + 3) ⋮ (x + 1)

A. x ∈ {-3; -2; 0; 1}

B. x ∈ {-1; 0; 2; 3}

C. x ∈ {-3; 0; 1; 2}

D. x ∈ {-2; 0; 1; 3}

Đáp án

Câu 9: Tìm số nguyên x biết 3|x + 1| = 9 :

A. x = 2

B. x = -4

C. Cả A và B

D. Đáp án khác

Đáp án

Câu 10: Tìm số nguyên x biết (-12)².x = 56 + 10.13x

A. 3

B. 4

C. 5

D. 6

Đáp án