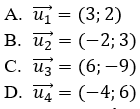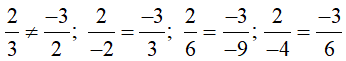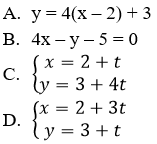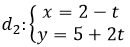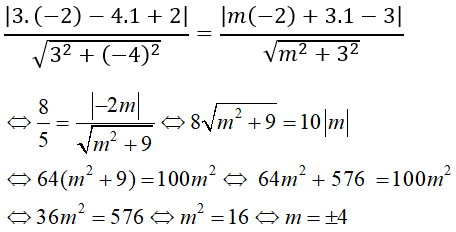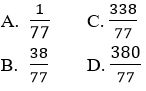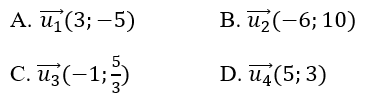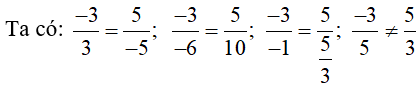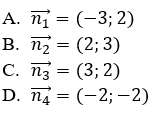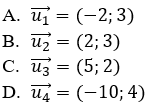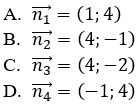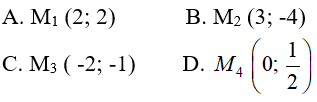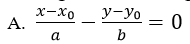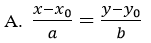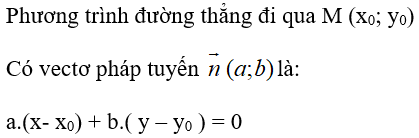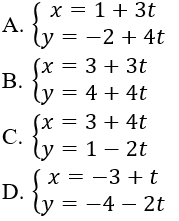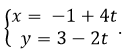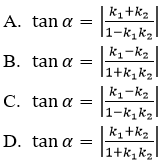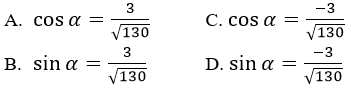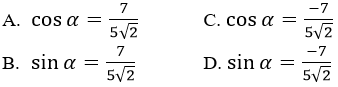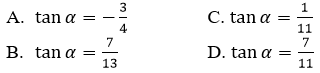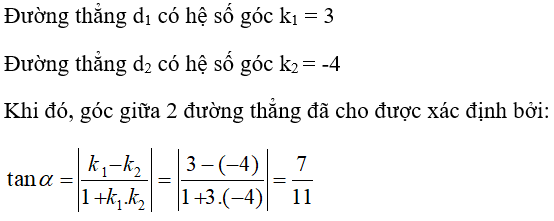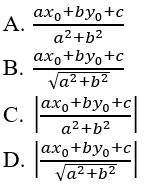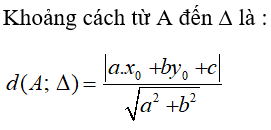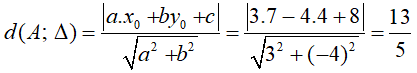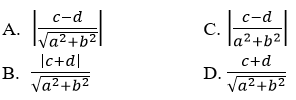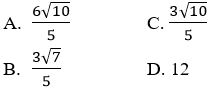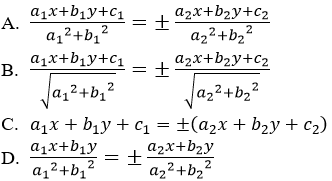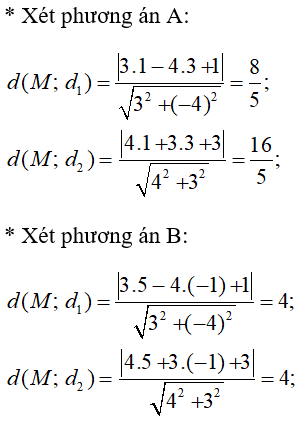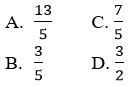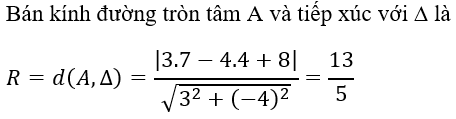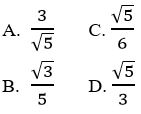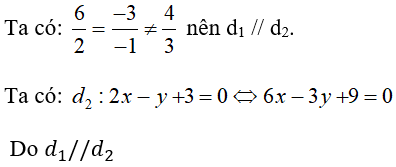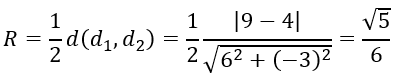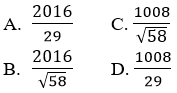Trắc nghiệm Toán học 10 Phương trình đường thẳng có đáp án năm 2021 - 2022
Bộ câu hỏi trắc nghiệm Toán học lớp 10 có đáp án, chọn lọc năm 2021 – 2022 mới nhất gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao. Hy vọng với tài liệu trắc nghiệm Toán học lớp 10 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 10
Trắc nghiệm Toán học 10: Phương trình đường thẳng
Câu 1: Cho đường thẳng Δ có vectơ chỉ phương là u→=(2;-3). Vectơ nào sau đây không phải là vectơ chỉ phương của Δ?
Đáp án A
Nếu u→ là vectơ chỉ phương của một đường thẳng thì ku→ (với k ≠ 0) đều là vectơ chỉ phương của đường thẳng đó.
Vì vậy các vectơ có tọa độ tỉ lệ với u→=(2;-3) đều là vectơ chỉ phương.
Ta có:
Do đó, trong các vectơ đã cho có u1→ không phải là vectơ chỉ phương của đường thẳng ∆.
Câu 2: Phương trình tham số của đường thẳng Δ đi qua điểm M(2; 3) và có hệ số góc k = 4 là:
Đáp án C
Đường thẳng Δ có hệ số góc k = 4 nên có vectơ chỉ phương u→ = (1;4). Do đó C là phương án đúng.
Chú ý. Học sinh có thể nhầm sâng các loại phương trình khác của đường thẳng như các phương án ở A và B. Đây đều là phương trình của đường thẳng nhưng không là phương trình tham số.
Câu 3: Cho hai đường thẳng d1: 3x – 4y +2 = 0 và d2: mx +2y – 3 = 0. Hai đường thẳng song song với nhau khi:
A. m = 3
B. m=3/2
C. m=-3/2
D. m = - 3
Đáp án C
Hai đường thẳng song song khi:
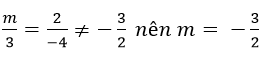
Câu 4: Cho hai đường thẳng d1: y = 3x – 1 và
Góc giữa hai đường thẳng là:
A. α = 30o
B. α=45o
C. α=60o
D. α=90o
Đáp án B
Hai đường thẳng lần lượt có các vectơ chỉ phương là u1→=(1;3) và u2→=(-1;2) nên ta có
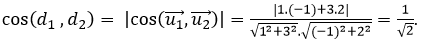
Do đó góc giữa hai đường thẳng là α = 45o.
Câu 5: Cho điểm A(-2; 1) và hai đường thẳng d1: 3x – 4y + 2 = 0 và d2: mx + 3y – 3 = 0. Giá trị của m để khoảng cách từ A đến hai đường thẳng bằng nhau là:
A. m=±1
B. m = 1 và m = 4
C. m=±4
D. m = - 1 và m = 4
Đáp án C
Sử dụng công thức khoảng cách ta có:
Chú ý. Học sinh có thể thử lại các phương án được đưa ra để chọn đáp án đúng, tuy nhiên sẽ tốn nhiều thời gian hơn là làm bài toán trực tiếp.

Câu 6: Cho tam giác ABC với A(-2; 3), B(1; 4), C(5; -2). Phương trình đường trung tuyến AM của tam giác là:
A. x – 2y + 8 = 0
B. 2x + 5y – 11 = 0
C. 3x – y + 9 = 0
D. x + y – 1 = 0
Đáp án B
Câu 7: Cho tam giác ABC có phương trình các cạnh AB: 3x – y + 4 = 0, AC: x + 2y – 4 = 0, BC: 2x + 3y – 2 = 0. Khi đó diện tích của tam giác ABC là:
Đáp án C
Bằng việc lần lượt giải các hệ phương trình bậc nhất hai ẩn, ta có tọa độ các đỉnh của tam giác là
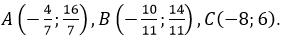
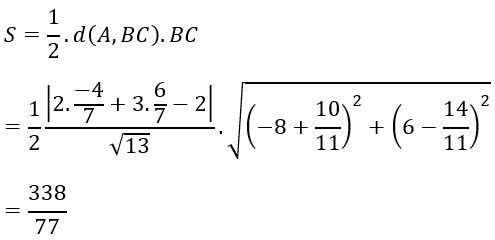
Ta có công thức tính diện tích tam giác ABC là:
Câu 8: Cho điểm A(3; 5) và các đường thẳng d1: y = 6, d2: x = 2. Số đường thẳng d qua A tạo với các đường thẳng d1, d2 một tam giác vuông cân là
A. 0
B. 1
C. 2
D. Vô số
Đáp án B
Do d1 ⊥ d2 nên d có tính chất trên thì d tạo với tía Ox góc 45o hoặc 135o. Mà d1, d2 cắt nhau tại B(2; 6) nên AB tạo với Ox góc 135o. Do đó, trong hai đường thẳng kề trên chỉ có đường thẳng tạo với Ox góc 45o thỏa mãn yêu cầu, còn đường thẳng tạo với Ox góc 135o phải loại bỏ do khi đó không tạo thành tam giác. Đáp án là phương án B.
Chú ý. Học sinh thường quên xét góc của AB tạo với Ox và chọn luôn phương án là hai đường thẳng.
Câu 9: Có bao nhiêu vectơ pháp tuyến của một đường thẳng?
A. 0
B. 1
C. 2
D. Vô số
Đáp án D
Nếu n→ là vectơ pháp tuyến của một đường thẳng thì kn→ (với k ≠ 0) đều là vectơ pháp tuyến của đường thẳng.
Vì thế có vô số vectơ pháp tuyến của một đường thẳng.
Câu 10: Cho đường thẳng Δ có một vectơ chỉ phương là u→(-3;5). Vectơ nào dưới đây không phải là VTCP của Δ?
Đáp án D
Các vectơ khác vectơ – không, cùng phương (tọa độ tỉ lệ) với u→ thì đều là VTCP của đường thẳng Δ.
Do đó vectơ ở phương án D không phải là VTCP.
Câu 11: Cho đường thẳng Δ có vectơ chỉ phương là u→=(2;-3). Vectơ nào sau đây là vectơ pháp tuyến của Δ?
Đáp án C
Gọi u→; n→ lần lượt là vectơ chỉ phương và vectơ pháp tuyến của đường thẳng ∆:
Câu 12: Cho đường thẳng Δ có phương trình
Vectơ nào sau đây là vectơ chỉ phương của Δ?
Đáp án D
Câu 13: Cho đường thẳng Δ có phương trình y = 4x – 2. Vectơ nào sau đây là vectơ pháp tuyến của Δ?
Đáp án B
Đường thẳng Δ có phương trình y = 4x – 2 ⇔ 4x – y – 2 = 0 nên có một vectơ pháp tuyến là n→=(4;-1)
Câu 14: Cho đường thẳng Δ có phương trình 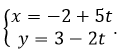
Đáp án B
Điểm nằm trên đường thẳng ∆ nếu tọa độ điểm thỏa mãn phương trình đường thẳng ứng với một giá trị t nào đó.
Câu 15: Cho đường thẳng Δ có phương trình 3x – 4y + 2 = 0. Điểm nào sau đây không nằm trên đường thẳng Δ?
Đáp án B
Câu 16: Một đường thẳng có bao nhiêu phương trình tham số?
A. 0
B. 1
C. 2
D. Vô số
Đáp án D
Phương trình tham số tùy thuộc vào điểm được chọn trên đường thẳng và vectơ chỉ phương của đường thẳng.
Mà 1 đường thẳng có vô số điểm và có vô số vectơ chỉ phương nên có vô số phương trình tham số của đường thẳng.
Câu 17: Phương trình của đường thẳng qua điểm M(x0; y0) có vectơ chỉ phương u→=(a;b) là:
A. b(x-x0 ) - a(y-y0 )=0
B. a(x+x0 ) + b(y+y0 )=0
C. a(x-x0 ) + b(y-y0 )=0
Đáp án B
Đường thẳng có vectơ pháp tuyến n→=(b;-a) nên phương trình của đường thẳng là b(x-x0)-a(y-y0)=0
Câu 18: Phương trình của đường thẳng qua điểm M(x0 ;y0 ) có vectơ pháp tuyến n→=(a;b) là:
A. b(x - x0) - a(y - y0) = 0
B. a(x + x0) + b(y + y0) = 0
C. a(x - x0) + b(y - y0) = 0
Đáp án D
Câu 19: Phương trình tham số của đường thẳng Δ đi qua điểm M(3; 4) và có vectơ chỉ phương là u→ = (3;4) là:
Đáp án B
Câu 20: Phương trình tổng quát của Δ đi qua điểm M(3;4) và có vectơ pháp tuyến n→=(1;-2)là:
A. 3(x + 1) + 4(y – 2) = 0
B. 3(x – 1) + 4(y + 2) = 0
C. (x – 3) – 2(y – 4) = 0
D. (x + 3) – 2(y + 4) = 0
Đáp án C
Câu 21: Phương trình tham số của đường thẳng Δ đi qua điểm M(3; 4) và song song với đường thẳng 2x – y + 3 = 0 là:
A. 2x – y – 3 = 0
B. 2x – y + 5 = 0
C. 2x – y – 2 = 0
D. 2x – y
Đáp án C
Câu 22: Phương trình tham số của đường thẳng Δ đi qua điểm M1(3;4 ) và vuông góc với đường thẳng 2x – y + 3 = 0 là:
A. x – 2y + 5 = 0
B. x + 2y – 11 = 0
C. 2x – y – 2 = 0
D. 2x – y = 0
Đáp án B
Câu 23: Cho đường thẳng Δ có phương trình tham số là
Phương trình nào sau đây là phương trình tổng quát của ∆?
A. x – 2y + 5 = 0
B. x + 2y – 11 = 0
C. x + 2y – 5 = 0
D. x – y = 0
Đáp án C
Câu 24: Cho đường thẳng Δ có phương trình tổng quát là 2x – y – 2 = 0. Phương trình nào sau đây là phương trình tham số của Δ?
Đáp án D
Chú ý. Do phương trình tham số của đường thẳng là không duy nhất nên ta sẽ đi kiểm tra các phương án trả lời được đưa ra thay cho việc tiến hành viết phương trình tham số của đường thẳng.
Câu 25: Cho điểm A(3; 4), B(-1; 2). Phương trình của đường thẳng AB là:
A. x – 2y + 5 = 0
B. 2x + y – 5 =0
C. x + 2y – 5 = 0
D. 2x – y =0
Đáp án A
Câu 26: Cho điểm A(3; 4), B(-1; 2). Phương trình đường thẳng trung trực của đạon thẳng AB là:
A. x – 2y + 5 = 0
B. 2x + y – 5 =0
C. x + 2y – 5 = 0
D. 2x + y – 1 =0
Đáp án B
Câu 27: Cho ba điểm A(3;2), B(1;-2), C(4;1). Đường thẳng qua A và song song với cạnh BC có phương trình là:
A. x – y + 5 = 0
B. x + y – 5 = 0
C. x – y – 1 = 0
D. x + y = 0
Đáp án C
Câu 28: Cho ba điểm A(3;2), B(1;-2), C(4;1). Đường thẳng qua A và vuông góc với cạnh BC có phương trình là:
A. x – y + 5 = 0
B. x + y – 5 = 0
C. x – y – 1 = 0
D. x + y = 0
Đáp án B
Câu 29: Cho điểm A(1;3) và đường thẳng d: 2x – 3y + 4 = 0. Số đường thẳng qua A và tạo với d một góc 60o là:
A. 0
B. 1
C. 2
D. Vô số
Đáp án C
Phương trình (*) có 2 nghiệm phân biệt. Ứng với mỗi nghiệm ta tìm được 1 cặp số (a, b) là VTPT của đường thẳng ∆. Từ đó, ta viết được 2 phương trình đường thẳng ∆ thỏa mãn.
Câu 30: Cho điểm A(1;3) và đường thẳng d: x – y + 4 = 0. Số đường thẳng qua A và tạo với d một góc 45o là:
A. y – 1 = 0 và x – 3 = 0
B. x + 1 = 0 và y + 3 = 0
C. y – 3 = 0 và x – 1 = 0
D. Không có
Đáp án C
Câu 31: Cho điểm A(1; 3) và hai đường thẳng d1:2x-3y+4=0,d2:3x+y=0. Số đường thẳng qua A và tạo với d1,d2 các góc bằng nhau là
A. 1
B. 2
C. 4
D. Vô số
Đáp án B
Đường thẳng qua A và tạo với d1,d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1, d2.
Do vậy số lượng đường thẳng cần tìm là 2.
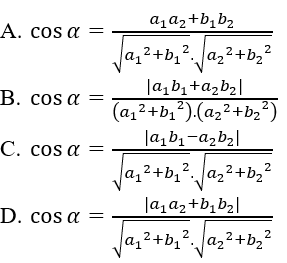
Câu 32: Cho α là góc tạo bởi hai đường thẳng d1: a1x + b1y + c1 = 0 và d2:a2x + b2y + c2=0. Khẳng định nào sau đây là đúng?
Đáp án D
Câu 33: Cho α là góc tạo bởi hai đường thẳng d1: y=k1x + m1 và d2: y=k2y + m2. Khẳng định nào sau đây là đúng?
Đáp án B
Câu 34: Cho α là góc tạo bởi hai đường thẳng d1: 2x-3y+4=0 và d2: 3x+y=0. Khẳng định nào sau đây là đúng?
Đáp án A
Câu 35: Cho α là góc tạo bởi hai đường thẳng d1: x+3y+4=0 và d2: 2x-y=0. Khẳng định nào sau đây là đúng?
Đáp án B
Câu 36: Cho α là góc tạo bởi hai đường thẳng d1: y=3x+5 và d2: y=-4x+1. Khẳng định nào sau đây là đúng?
Đáp án D
Câu 37: Cho điểm A(x0;y0) và đường thẳng Δ: ax + by + c = 0. Khoảng các từ A đến đường thẳng Δ được cho bởi công thức
Đáp án D
Câu 38: Cho điểm A(7; 4) và đường thẳng Δ: 3x – 4y + 8 = 0. Khoảng cách từ A đến đường thẳng Δ là
A. 2
B. 3/5
C. 13/5
D. 3/2
Đáp án C
Câu 39: Khoảng cách giữa hai đường thẳng d1: ax+by+c=0 và d2: ax+by+d=0 được cho bởi công thức nào sau đây?
Đáp án A
Khi 2 đường thẳng song song với nhau thì khoảng cách giữa hai đường thẳng đó bằng khoảng cách từ 1điểm bất kì nằm trên đường thẳng này đến đường thẳng kia.
Câu 40: Khoảng cách giữa hai đường thẳng d1: x+3y-5=0 và d2: x+3y+7=0 được cho bởi công thức nào sau đây?
Đáp án A
Câu 41: Khoảng cách giữa hai đường thẳng d1: 6x-4y+5=0 và d2: 3x-2y+1=0 được cho bởi công thức nào sau đây?
Đáp án D
Câu 42: Cho hai đường thẳng cắt nhau d1: a1x+b1y+c1=0 và d2: a2x+b2y+c2=0. Phương trình các phân giác góc tạo bởi d1,d2 là
Đáp án B
Câu 43: Cho hai đường thẳng cắt nhau d1: 3x-4y+1=0 và d2: x+3=0. Phương trình các phân giác góc tạo bởi d1,d2 là
A. x + 2y + 7 = 0 và 2x – y + 7 = 0
B. x + 2y + 4 = 0 và 2x – y + 4 = 0
C. x + 2 y + 7 = 0 và 2x – y + 4 = 0
D. x + 2y – 7 = 0 và 2x – y – 7 = 0
Đáp án C
Câu 44: Cho hai đường thẳng d1:3x-4y+1=0,d2:4x+3y+3=0. Điểm M nào sau đây cách đều hai đường thẳng trên?
A. M(1;3)
B. M(5; -1)
C. M(4; -2)
D. M(-1; 2)
Đáp án B
Cách 1. Viết phương trình 2 đường phân giác tạo bởi 2 đường thẳng đã cho.
Khi đó, điểm nào nằm trên hai đường phân giác này thì cách đều hai đường thẳng đã cho.
Cách 2. Tính khoảng cách từng điểm đến hai đường thẳng.
Do đó, điểm M(5; -1) cách đều hai đường thẳng đã cho.
Câu 45: Cho ba đường thẳng d1:3x-4y+1=0,d2:5x+3y-1=0,d3:x+y+6=0. Số điểm M cách đều ba đường thẳng trên là
A. 1
B. 2
C. 3
D. 4
Đáp án D
Do các đường thẳng đôi một cắt nhau tại các điểm A, B, C nên các điểm cách đều các cạnh gồm tâm đường tròn nội tiếp và ba tâm đường tròn bàng tiếp.
Vậy có tất cả 4 điểm M cách đều ba đường thẳng đã cho.
Câu 46: Cho ba đường thẳng d1:3x-4y+1=0,d2:x-5y-3=0,d3:-6x+8y+1=0. Số điểm M cách đều ba đường thẳng trên là
A. 1
B. 2
C. 3
D. 4
Đáp án B
Do d1 song song với d3 nên những điểm cách đều chúng nằm trên đường thẳng ∆ song song cách đều d1, d3.
Gọi khoảng cách hai đường thẳng d1, d3 là a > 0.
Khoảng cách giữa 2 đường thẳng ∆ và d1; ∆ và d3 là a/2
Gọi giao điểm của ∆ và d2 là A. Trên đường thẳng ∆ có 2 điểm B; C thỏa mãn AB = AC = a/2
Hai điểm B và C là 2 điểm cần tìm.
Số điểm M cách đều ba đường thẳng là 2.
Câu 47: Cho điểm A(7; 4) và đường thẳng Δ: 3x – 4y + 8 = 0. Bán kính đường tròn tâm A và tiếp xúc với Δ là:
Đáp án A
Câu 48: Cho hai đường thẳng d1:x-3y+4=0,d2:2x-y+3=0. Bán kính đường tròn tiếp xúc với hai đường thẳng d1,d2 là
Đáp án C
Nên khoảng cách hai đường thẳng d1 và d2 chính là đường kính của đường tròn.
Suy ra, bán kính đường tròn tiếp xúc với hai đường thẳng d1, d2 là
Câu 49: Cho tam giác ABC, biết phương trình ba cạnh của tam giác là
AB: x – 3y – 1 = 0, BC: x + 3y + 7 = 0, CA: 5x – 2y + 1 = 0
Phương trình đường cao AH của tam giác là:
A. 13x – 39y + 9 = 0
B. 39x – 13 y + 9 = 0
C. 39x – 13y – 9 = 0
D. 39x + 13y + 9 = 0
Đáp án B
Câu 50: Cho ba điểm A(5;2), B(1; - 4), C(3; 6). Phương trình trung tuyến AM của tam giác là:
A. x – 3y + 1 = 0
B. 3x – y + 1 = 0
C. x – y + 1 = 0
D. 3x – 3y + 1 = 0
Đáp án A
Câu 51: Nếu m là số đường thẳng Δ có tính chất đi qua điểm M(8; 5) và cắt Ox, Oy tại A, B mà OA = OB thì
A. m = 0
B. m = 1
C. m = 2
D. m = 3
Đáp án C
Câu 52: Cho hai đường thẳng d1: (√3+1)x+(3-√2)y+1=0,d2: √5 x+(4-√2)y-6=0.
Khẳng định nào sau đây là đúng?
A. Hai đường thẳng trùng nhau
B. Hai đường thẳng song song
C. Hai đường thẳng cắt nhau
D. Hai đường thẳng vuông góc với nhau
Đáp án C
Câu 53: Cho hai đường thẳng d1:2x+3y+1=0,d2:mx+(2m-2)y-m+6=0. Giá trị của m để hai đường thẳng song song là
A. m =0
B. m = - 4
C. m = 4
D. không tồn tại m thỏa mãn
Đáp án D
Câu 54: Cho ba đường thẳng d1: 2x+3y+1=0,d2: mx+(m-1)y-2m+1=0,d3: 2x+y-5=0. Giá trị của m để hai đường thẳng d1,d2 cắt nhau tại một điểm nằm trên d3 là:
A. m = 0
B. m = - 4
C. m = 4
D. không tồn tại giá trị m thỏa mãn
Đáp án C
Câu 55: Cho ba đường thẳng d1:x-2y+1=0,d2:mx-(3m-2)y+2m-2=0,d3:x+y-5=0. Giá trị m để hai đường thẳng d1,d2 cắt nhau tại một điểm nằm trên d3 là
A. m = 0
B. m = 1
C. m = 2
D. không tồn tại m thỏa mãn
Đáp án D
Câu 56: Cho hai đường thẳng d: (m – 2)x +(m – 6)y + m – 1= 0, Δ: (m – 4)x + (2m – 3)y – m + 5 = 0. Tất cả giá trị của m để hai đường thẳng cắt nhau là
A. m ≠ 3
B. m ≠ 6
C. m ≠ 3 và m ≠ -6
D. không có m thỏa mãn
Đáp án C
Câu 57: Cho hình chữ nhật ABCD có đỉnh A(7; 4) và phương trình hai cạnh là:
7x – 3y + 5 = 0, 3x + 7y – 1 = 0. Diện tích hình chữ nhật ABCD là:
Đáp án D
Câu 58: Diện tích hình vuông có bốn đỉnh nằm trên hai đường thẳng song song d1:2x-4y+1=0 và d2:-x+2y+10=0 là:
Đáp án D
Do 4 đỉnh hình vuông nằm trên 2 đường thẳng song song nên độ dài cạnh hình vuông chính là khoảng cách giữa hai đường thẳng song song
Câu 59: Cho tam giác ABC với A(-1; -1), B(2; -4), C(4; 3). Diện tích tam giác ABC là:
A. 3/2
B. 9/2
C. 27/2
D. 13
Đáp án C
Câu 60: Cho hai điểm A(-4; -1), B(-2; 1). Điểm C trên đường thẳng ∆: x – 2y + 3 = 0 sao cho diện tích tam giác ABC bằng 40 (đvdt). Khi đó tung độ của điểm C là
A. – 10 hoặc 10
B. – 40 hoặc 40
C. 20
D. 50
Đáp án B