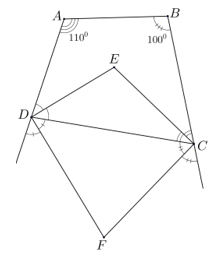
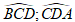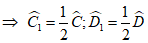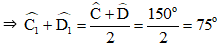Tứ giác ABCD có A = , B = . Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau tại F. Tính (CED), CFD
Quảng cáo
1 câu trả lời 535
Trong tứ giác ABCD, ta có: A + B + C + D =
⇒ C + D = - (A + B) = – ( + ) =
Do DE và CE lần lượt là tia phân giác của góc
Trong ΔCED ta có:
CED = 180o – =
DE ⊥ DF (t/chất tia phân giác của hai góc kề bù) ⇒ EDF =
CE ⊥ CF (t/chất tia phân giác của hai góc kề bù) ⇒ ECF =
Trong tứ giác CEDF, ta có: DEC + EDF + DFC + ECF =
⇒ DFC = - (DEC + EDF + ECF) =
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915
Gửi báo cáo thành công!