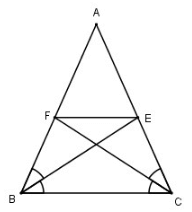
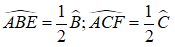Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
Quảng cáo
1 câu trả lời 565
+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
Mà tam giác ABC cân tại A nên B = C
Suy ra: ABE = ACF
Xét hai tam giác AEB và AFC
Có AB = AC (ABC cân tại A)
ABE = ACF (chứng minh trên)
A là góc chung
⇒ AEB = AFC (g.c.g) ⇒ AE = AF ⇒ AEF cân tại A
⇒ AFE = (− A) / 2 và trong tam giác ABC: B = (− ∠A) / 2
⇒AFE = B ⇒ FE//BC ( có hai góc ở vị trí đồng vị bằng nhau).
⇒ Tứ giác BFEC là hình thang.
Vì FE//BC nên ta có: FEB = EBC (so le trong)
Lại có: FBE = EBC ( vì BE là tia phân giác của góc B)
⇒FBE = FEB
⇒ FBE cân ở F ⇒ FB = FE
⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915