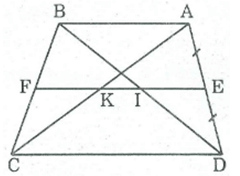
Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai.
Quảng cáo
1 câu trả lời 996
Xét hình thang ABCD có AB // CD.
E là trung điểm AD, đường thẳng đi qua E song song với AB cắt BC tại F, AC tại K, BD tại I.
Vì E là trung điểm AD nên EF// AB
Suy ra: BF = FC (tính chất đường trung bình hình thang)
Trong ADC ta có: E là trung, điểm của cạnh AD
EK // DC
Suy ra: AK = KC (tính chất đường trung bình của tam giác)
Trong ABD ta có: E là trung điểm của cạnh AD
EI // AB
Suy ra: BI = ID (tính chất đường trung bình của tam giác)
Vậy đường thẳng song song với 2 đáy, đi qua trung điểm E của cạnh bên AD của hình thang ABCD thì đi qua trung điểm của cạnh bên BC và trung điểm hai đường chéo AC, BD.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17097
Đã trả lời bởi chuyên gia
17097 -
 Đã trả lời bởi chuyên gia
16079
Đã trả lời bởi chuyên gia
16079 -
 Đã trả lời bởi chuyên gia
10012
Đã trả lời bởi chuyên gia
10012 -
 Đã trả lời bởi chuyên gia
8884
Đã trả lời bởi chuyên gia
8884 -
 Đã trả lời bởi chuyên gia
8830
Đã trả lời bởi chuyên gia
8830 -
 Đã trả lời bởi chuyên gia
7498
Đã trả lời bởi chuyên gia
7498 -
 Đã trả lời bởi chuyên gia
5904
Đã trả lời bởi chuyên gia
5904