Question

Đã trả lời bởi chuyên gia

Answer 1

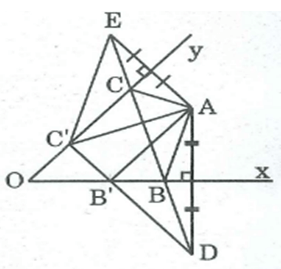
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Cách dựng:

- Dựng điểm D đối xứng với A qua Ox

- Dựng điểm E đối xứng với A qua Oy

Nối DE cắt Ox tại B, Oy tại C

Tam giác ABC là tam giác có chu vi nhỏ nhất

Vì $∠$ (xOy) < $90^{0}$ nên DE luôn cắt Ox và Oy do đó $∆$ ABC luôn dựng được.

Chứng minh:

Chu vi $∆$ ABC bằng AB + BC + AC

Vì D đối xứng với A qua Ox nên Ox là trung trực của AD

⇒ AB = BD (tính chất đường trung trực)

E đối xứng với A qua Oy nên Oy là trung trực của AE

⇒ AC = CE (tính chất đường trung trực)

Suy ra: AB + BC + AC = BD + BC + BE = DE (1)

Lấy B' bất kì trên Ox, C' bất kì trên tia Oy. Nối C'E, C'A, B'A, B'D.

Ta có: B'A = B'D và C'A = C'E (tính chất đường trung trực)

Chu vi $∆$ AB'C' bằng AB'+ AC’ + B'C'= B'D+C’E+ B'C' (2)

Vì DE ≤ B'D + C’E+ B'C' (dấu bằng xảy ra khi B' trùng B, C' trùng C) nên chu vi của $∆$ ABC $\leq$ chu vi của $∆$ A'B'C'

Vậy $∆$ ABC có chu vi bé nhất.

...Xem thêm

Answer 2