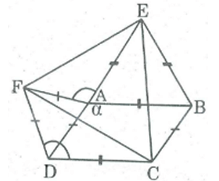
Cho hình bình hành ABCD có A = > . Ở phía ngoài hình bình hành vẽ các tam giác đều ADF, ABE. Chứng minh rằng tam giác CEF là tam giác đều.
Quảng cáo
1 câu trả lời 560
Ta có:
(BAD) + ∠(ADC) = (hai góc trong cùng phía bù nhau)
⇒ (ADC) = - (BAD) = –
(CDF) = (ADC) + (ADF) = -
Suy ra: (CDF) = (EAF)
Xét AEF và DCF: AF = DF ( vì ADF đều)
AE = DC (vì cùng bằng AB)
(CDF) = (EAF) (chứng minh trên)
Do đó: AEF = DCF (c.g.c) ⇒ EF = CF (1)
(CBE) = (ABC) +
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
(CBE) = (CDF) =
BC = DF (vì cùng bằng AD)
Do đó BCE = DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ECF đều.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915
Gửi báo cáo thành công!