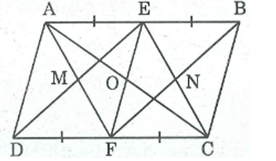
Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng: EMNF là hình bình hành
Quảng cáo
1 câu trả lời 281
+) Ta có:
AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).
Và AB = CD (tính chất hình bình hành)
Suy ra: AE = CF
+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF
Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành
⇒ AF //CE hay EN // FM (1)
Xét tứ giác BFDE ta có:
AB // CD (gt) hay BE // DF
BE = 1/2 AB (gt)
DF = 1/2 CD (gt)
AB = CD (tính chất hình bình hành)
Suy ra: BE = DF
Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)
Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915